描述性统计是最基础但同时也是最重要的数据分析之一,这一步做不好,之后的高端复杂模型根本不用考虑的——连数据统计分布都分析不对,之后的复杂模型肯定是错的。主要再这里介绍下面一些东西:
- 描述性统计分析
- 离散程度的度量
- 分组进行描述性统计分析
- 查看分布
在做数据分析时,一般先会对数据进行描述性统计分析,以便于描述该数据的各种特征及其所代表的总体的特征。描述性统计分析包括对数据的集中趋势、离散程度以及分布进行分析。
- 集中趋势统计量: 均值(Mean)、中位数(Median)、众数(Mode)、百分位数
- 离散趋势统计量:标准差(sd)、方差(var)、极差(range)、变异系数(CV)、标准误、样本校正平方和(CSS)、样本未校正平方和(USS)
- 分布情况统计量:偏度、峰度
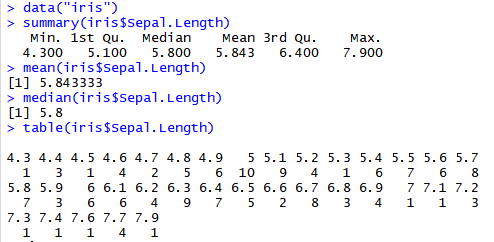
其中代码都非常简单,mean函数计算均值,median函数计算中位数,table计算不同数据出现的频率。
这里我们用测试数据集鸢尾花的数据(iris)
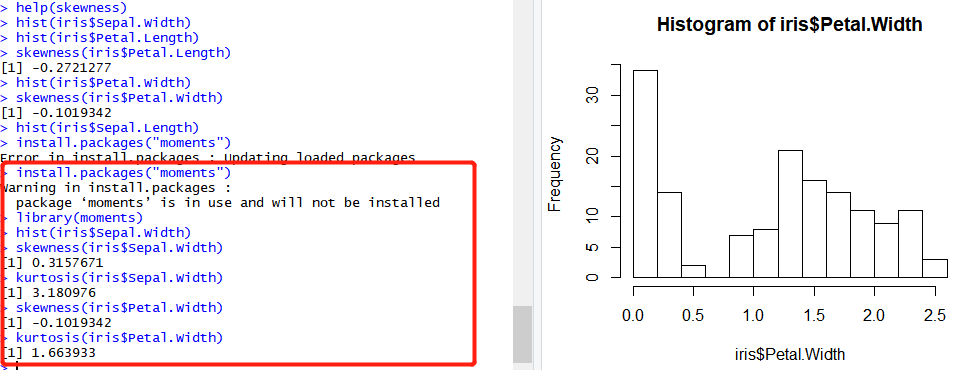
分布情况统计是很重要的两个指标,具体来说就是,偏度(skew)可以告诉你,这批数据有没有做左偏还是右偏了,峰度(kurtosis)可已告诉你这批数据是尖尖山峰的还是矮矮的山包。
其实偏度和峰度的计算公式都很简单,不过我们可以使用moments包来计算偏度和峰度:
离散程度的度量:
离散系数又称变异系数,是统计学当中的常用统计指标,主要用于比较不同水平的变量数列的离散程度及平均数的代表性。离散系数指标有:全距(极差)系数、平均差系数、方差系数和标准差系数等。常用的是标准差系数,用CV(Coefficient of Variance)表示。CV(Coefficient of Variance):标准差与均值的比率。
用公式表示为:
CV=σ/μCV=σ/μ
这个公式很好理解,上半部是标准差,下边的分母是均值。
其现实意义就是,这样的标准差再这样的均值上是一个怎么样的程度:比如说如果玉米粒之间的重量方差是到1g,汽车之间的重量方差是10kg,那么到底这两个东西之间的离散程度谁比较大呢?我们很明显能感觉到,我们之所以感到矛盾,是因为感觉汽车本来就比玉米粒重太多,所以也许对于汽车来说,10kg的差异是很小的,但是玉米粒本来就很轻,所以对于玉米粒来说,可能1g的差异已经很大了。所以用标准差与均值做除数,就可以让我们比较不同数据之间的离散程度。
此外,还有一些其他用于计算离散程度的指标:
极差(全距)系数:Vr=R/X′Vr=R/X′;
平均差系数:Va,d=A.D/X′Va,d=A.D/X′;
方差系数:V方差=方差/X′V方差=方差/X′;
标准差系数:V标准差=标准差/X′V标准差=标准差/X′;
其中,X′X′表示XX的平均数。
就我个人而言,我感觉拿到一批数据,判断一下它离散程度最好办法,就是直接一个boxplot画出来。

分组进行描述性统计分析
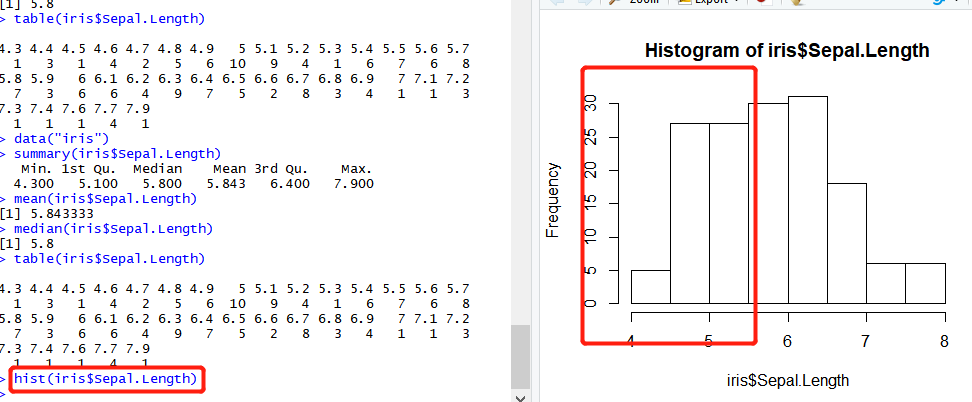
刚才我们演示了如何计算一批数据的基本统计量,有一个问题是,如果我们有几批数据,如何同时计算他们的描述性统计量?R语言提供了一个很好用的函数summary来解决这个问题:
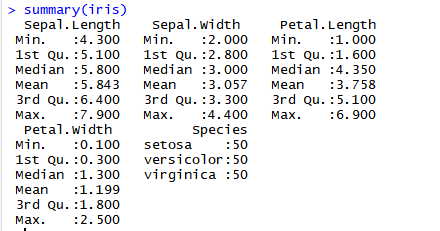
在这个统计结果中,min是最小值,1st Qu是下四分位点,median是中位数,mean是均值,3rd Qu是上四分卫数,max是最大数值。
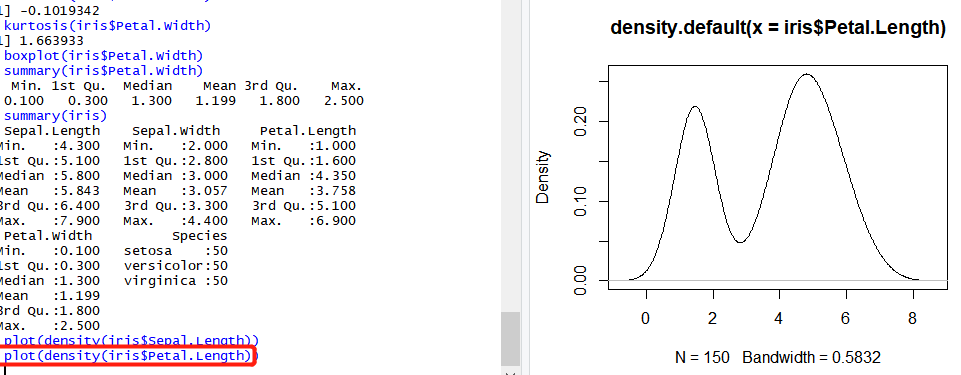
查看分布
绘制数据的分布图,是非常有用的一个方法去查看数据。而且代码极为简单,就是plot(density(x)),其中x是你的数据,下面就是我们的例子: