线性回归用于通过对一个或多个解释变量(x)建模来预测或估计响应变量(y)的值。 变量必须是成对的，连续的，并假设它们之间具有线性关系。 该技术在预测分析中广泛流行。

线性回归的假设

1. 根据沿Y轴测量的实际值和预测值之间的差值计算的残差应遵循正态分布。

2. 对于解释变量的所有观测值，随机误差项有相同的方差。

3. 随机误差项彼此不相关。

4. 响应和预测变量之间的关系是线性和加性的。

5. 误差项（εε）之间应相互独立。

那么如何去在R里面去做线性拟合呢？

使用lm（）函数拟合线性模型，如下所示。 R中不需要加载额外的软件包以适应模型，但可能需要一些额外的软件包来获取诊断参数，例如VIF {来自汽车软件包}。 要预测的变量通常称为“因变量”或“响应变量”，而用于解释或预测响应变量的变量称为以下任一项 - “自变量”，“预测变量”，“ 预测变量，“解释变量”或“协变量”。

在下面的示例代码中，要预测的变量（因变量）被命名为“responseVar”，解释变量被命名为“pred1”，“pred2”等。您可以根据需要添加任意数量的解释变量。 让我们看看现在制作模型的代码

这里的模型对象是'fa'，在载入数据后的三行分别介绍了单项线性回归、多项线性回归和非截距回归的三种形式。

建模诊断

为了判断我们得到的这个模型具体表现如何，以下介绍了几个方式。

第1步：p值

p值应小于预定的显着性水平（通常为0.05）。如果p值小于0.05，您可以安全地拒绝零假设，即该变量的系数值为零（或者换句话说，拒绝预测变量与响应没有解释关系的零假设变量）。

检查变量的p值（显示在每个变量的右侧，标记为***）和模型（显示在摘要的最右下方（lmMod））理想情况下应该是诊断的第一步。 p值是用于在模型用于估计目的时验证模型的主要参数（找到测试数据的响应值）。

但是，可以认为p值大于显着性水平的模型可能仍然可用于预测目的。因此，在预测模型中，预测变量不一定纯粹基于p值被丢弃。

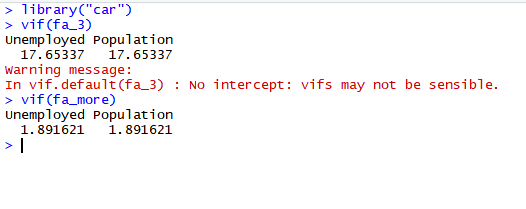
第2步：检查方差膨胀系数因子（VIF）

方差膨胀系数因子是指回归系数的估计量，由于自变量共线性使得方差增加的一个相对度量。

这里介绍VIF的计算方法，首先通过其他自变量的回归方程来预测关注的自变量，得到回归的R2值，那么这个关注自变量的VIF就是

VIF = 1/(1-R2)

较好的预测模型中我们希望保持VIF尽可能低，理想情况下小于2，高VIF（4及以上）表示该预测变量可由其他现有预测变量解释，因此该变量可能不是必需的。 这种情况被称为多共线性的存在。

第3步：检查残差的自相关性

这是建模时间相关数据（即因变量是时间序列）的必要步骤。 durbin-watson测试可用于检测随机干扰项是否自相关的。 这意味着，当前时间段中观察的误差项受前面某些时间段中的误差项的影响。 这意味着错误术语具有模式并且不是完全随机的，这也意味着，构建的模型没有解释因变量的某些部分（在错误中显示为自相关）计算。 这表明你应该调整你的模型，以便解释不明原因。 ARIMA模型能够解决这个问题。

D.W统计量是用来检验残差分布是否为正态分布的，因为进行回归估计是假设模型残差服从正态分布的，因此，如果残差不服从正态分布，那么，模型将是有偏的，也就是说模型的解释能力是不强的。
D.W统计量在2左右说明残差是服从正态分布的，若偏离2太远，那么你所构建的模型的解释能力就要受影响了。

第4步：检查AIC

AIC（Akaike信息标准）值越低，模型越好。 它有助于选择在模型的复杂性与拟合优度之间进行折衷的模型。

第5步：R平方和adj-R平方

R平方可以解释为由预测变量解释的响应变量的方差百分比。 因此，R-Sq越高，模型越好。 这也意味着，向模型添加更多预测变量总是会增加R平方值。 调整后的R平方会惩罚这种影响。 因此，使用adj-R Sq来比较从同一数据集构建的模型的解释力是一个好习惯。

此外，作为thumb规则，当给出模型选择时，选择具有较低AIC和较高的adj R Sq的较简单的模型。

第6步：获取预测变量的相对重要性（可选）

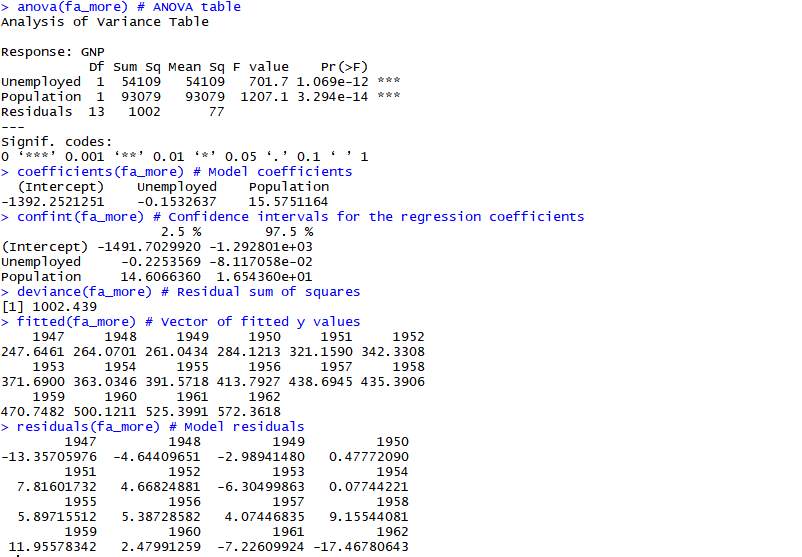
如何获得回归模型统计？

使用以下代码获取关键统计信息。

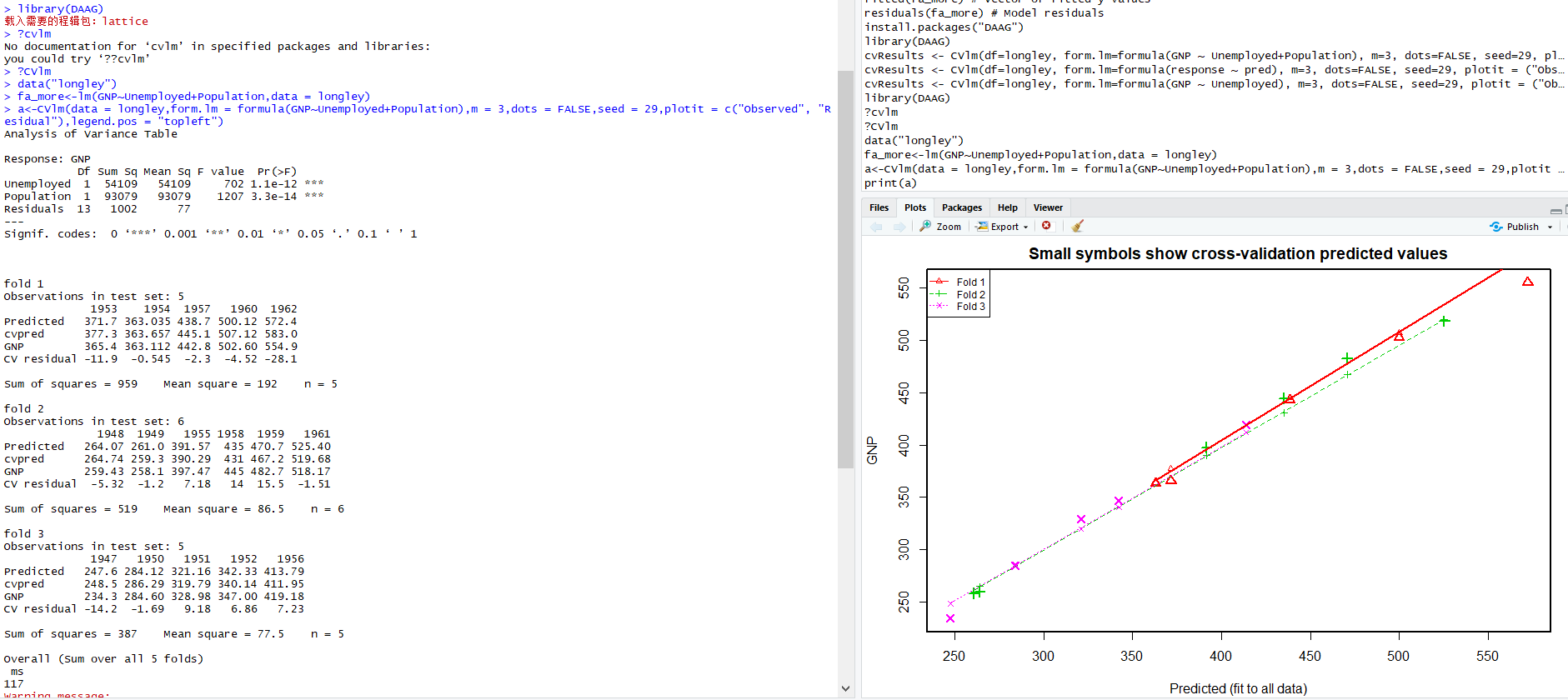
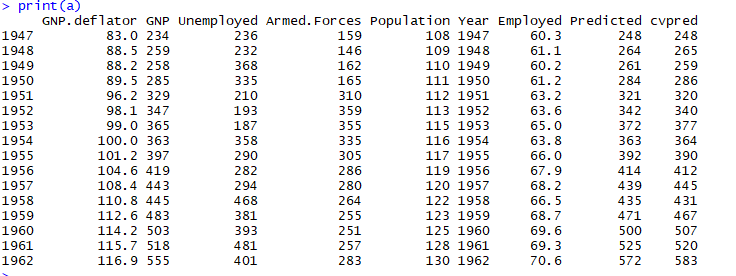
交叉验证

K-fold交叉验证将输入数据随机分成'k'折叠。 移除每个折叠后，重新拟合回归模型并用于预测删除的观察结果。