检查重要性:连续变量
对于每个连续预测变量,我们构建一个简单的回归模型。如果模型的p值小于预定的显着性水平,我们选择不拒绝变量,因此将其存储在'significantPreds_cont'中。这一步骤纯粹是为了限定有意义的变量,以便于我们构建更好的模型。
significantPreds_cont <- character() # 初始化输出,预测重要性将会存在这里
for (predName in names(inputData_cont)) {
pred <- inputData[, predName]
mod <- lm(response ~ pred) # 构建线性模型
p_value <- summary(mod)$coefficients[, 4][2] # 捕捉p值
if (p_value < 0.1 & p_value > 0) { # 对p值进行判断,其是否在(0,0.1)的区间
significantPreds_cont <- c (significantPreds_cont, predName) # 将结果存在significantPreds_cont
}
}
inputData_cont_signif <- inputData[, names(inputData) %in% significantPreds_cont] # 筛选出预测变量
检查重要性:分类变量
由于此处的因变量可以被视为序数计数变量,因此我们可以使用卡方检验来确定分类预测因子在解释因变量时是否重要。
在我们执行卡方检验(参见下面的代码)之后,如果p值变得小于预定的显着性水平,我们对分类变量进行限定并将其存储在'significantPreds_cat'中以进行进一步的步骤。
significantPreds_cat <- character() # 同样的初始化输出变量significantPreds_cat
for (predName in names(inputData_cat)) {
pred <- inputData[, predName]
chi_sq <- invisible(suppressWarnings(chisq.test(table(response, pred)))) # 进行卡方检验
p_value <- chi_sq[3] # capture p-Value
if (p_value < 0.1 & p_value > 0) { # 对p值进行判断,其是否在(0,0.1)的区间
significantPreds_cat <- c (significantPreds_cat, predName)
}
}
inputData_cat_signif <- as.data.frame(inputData[, names(inputData) %in% significantPreds_cat])
colnames(inputData_cat_signif) <- significantPreds_cat
将刚才通过筛选的变量和因变量放在一起,构建预测数据
inputData_signif <- cbind(response, inputData_cont_signif, inputData_cat_signif)
特征选择
第1部分:运用Boruta算法确定变量是否重要
boruta_output <- Boruta(response ~ ., data=na.omit(inputData_signif), doTrace=2) # 运行 Boruta方法
boruta_signif <- names(boruta_output$finalDecision[boruta_output$finalDecision %in% c("Confirmed", "Tentative")]) # 收集好确认和试验变量
第2部分:使用cforest算法根据精确度的平均下降估算出重要变量
cforest是我们可以用来找到最重要变量的众多技术之一。对于较小的数据,cforest比较方便。
cf1 <- cforest(response ~ . , data= na.omit(inputData_signif[, names(inputData_signif) %in% c(boruta_signif, "response")]), control=cforest_unbiased(mtry=2,ntree=50)) # 构建随机森林算法
impVars <- sort(varimp(cf1), decreasing=T) # 得到变量重要性
# 我们选择头7个变量
impVars <- if(length(impVars) > 7){
impVars[1:7]
} else {
impVars
}
第3部分:消除多重共线性
删除多重共线性,通过消除VIF值最高的变量,直到所有VIF都不超过4.由于分类变量中的每个级别在回归模型中使用时都会被视为单独的变量,因此我们不会将它们包含在VIF过滤中。
vars_considered_for_VIF_Filters <- names(impVars)[!names(impVars) %in% names(inputData_cat_signif)] #排除分类变量
fullForm <- (paste ("response ~ ", paste (vars_considered_for_VIF_Filters, collapse=" + "), sep=""))
fullMod <- lm(as.formula(fullForm), data=inputData_signif) # 构建线性模型
all_vifs <- try(vif(fullMod), silent=TRUE) # get all vifs
# 如果变量集中任何一个的vif值大于界限,就去除掉这个最大VIF的变量,直到所有变量都小于界限值
if(class(all_vifs) != "try-error"){
all_vifs <- as.data.frame(all_vifs)
while((nrow(all_vifs) > 2)& (max(all_vifs[, 1]) > 4) & (class(all_vifs) != "try-error")) {
remove_var <- rownames(all_vifs)[which(all_vifs[, 1] == max(all_vifs[, 1]))] # 找到最大的VIF变量
impVars <- impVars[!names(impVars) %in% remove_var] # 去除
fullForm <- paste ("response ~ ", paste (names(impVars), collapse=" + "), sep="") # 新公式
fullMod <- lm(as.formula(fullForm), data=inputData_signif) # 重构模型
all_vifs <- try(as.data.frame(vif(fullMod)), silent=TRUE) # 获得所有的VIF值
}
}
vif_filtered_variables <- names(fullMod$model)[!names(fullMod$model) %in% "response"]
现在,以下变量已被过滤为最适合解释臭氧读数的变量。当然我们也可以根据需求来调整上述的界限(如VIF级别,p值显着性级别等),获得一组不同的变量。
- pressure_height
- Inversion_base_height
- Humidity
- Month (tentative)
创建所选变量的所有组合,这些变量将作为预测变量进入模型
让我们构建所选预测变量的所有组合,以构建所有的模型。如果要限制模型的使用变量多少,可以在max_model_size变量中设置。
# create all combinations of predictors
max_model_size <- length(vif_filtered_variables)
combos_matrix <- matrix(ncol=max_model_size)
for (n in 1:length(vif_filtered_variables)){
combs_mat <- t(combn(vif_filtered_variables, n))
nrow_out <- nrow(combs_mat)
ncol_out <- length(vif_filtered_variables)
nrow_na <- nrow_out
ncol_na <- ncol_out-ncol(combs_mat)
na_mat <- matrix(rep(NA, nrow_na*ncol_na), nrow=nrow_na, ncol=ncol_na)
out <- cbind(combs_mat, na_mat)
combos_matrix <- rbind(combos_matrix, out)
}
combos_matrix <- combos_matrix[-1, ] # remove the first row that has all NA
构建训练集、预测集
set.seed(100)
trainingIndex <- sample(1:nrow(inputData_signif), 0.8*nrow(inputData_signif)) # 随机抽取80%作为训练集
inputData_signif_training <- na.omit(inputData_signif[trainingIndex, ]) #删掉含有na因变量的样本
inputData_signif_test <- na.omit(inputData_signif[-trainingIndex, ])
构建线性模型并诊断
现在我们完成了特征构建并得到预测变量的组合,我们可以期望从这些组合中生成几个好的模型。在下面的代码中,我们将首先构建模型,并在变量(currSumm)中捕获模型的整体情况。然后再利用如R-sq,p-Value,AIC等参数来诊断模型,最后,我们执行k-fold交叉验证并捕获模型的均方误差。我们从combos_matrix计算所有模型预测器组合的所有这些度量,它会在Final_Output数据框,并在Final_Regression_Output.csv文件中导出。除此之外,每个模型的模型概况,VIF和预测也会打印到控制台。
### 构建线性模型
Final_Output <- data.frame() # 构建输出数据集
for (rownum in 1:nrow(combos_matrix)){
## 从combos_matrix中构建模型
preds <- na.omit(combos_matrix[rownum, ])
form <- paste ("response ~ ", paste (preds, collapse=" + "), sep="")
currMod <- lm(as.formula(form), data=inputData_signif_training)
currSumm <- summary(currMod) # 模型概况
## 诊断的参数
f_statistic <- currSumm$fstatistic[1]
f <- currSumm$fstatistic
model_p <- pf(f[1], f[2], f[3], lower=FALSE) #模型的p值
r_sq <- currSumm[8] # R值
adj_r_sq <- currSumm[9] # R值校正
aic <- AIC(currMod) # AIC
bic <- BIC(currMod) # BIC
## 获得有影响力的观察值
cutoff <- 4/(nrow(inputData_signif_training)-length(currMod$coefficients)-2)
influential_obs_rownums <- paste(which(cooks.distance(currMod) > cutoff), collapse=" ")
## 在训练集上计算准确度
training_mape <- mean((abs(currMod$residuals))/abs(na.omit(inputData_signif_training$response))) * 100 # MAPE
actual_fitted <- data.frame(actuals=inputData_signif_training$response, fitted=currMod$fitted)
min_vals <- apply(actual_fitted, 1, min)
max_vals <- apply(actual_fitted, 1, max)
training_min_max <- min_vals/max_vals
training_min_max_accuracy <- mean(training_min_max)
## 在测试集上计算准确度
predicteds <- predict(currMod, inputData_signif_test) # 对训练集进行预测
predicted_mape <- mean((abs(inputData_signif_test$response - predicteds)/abs(inputData_signif_test$response))) * 100
actual_predicteds <- data.frame(actuals=inputData_signif_test$response, predicted=predicteds)
min_vals <- apply(actual_predicteds, 1, min)
max_vals <- apply(actual_predicteds, 1, max)
predicted_min_max <- min_vals/max_vals
predicted_min_max_accuracy <- mean(min_vals/max_vals) # 测试集的min-max准确值
## 实行k折交叉验证
par(mar=c(2,0,4,0))
cvResults <- suppressWarnings(CVlm(df=na.omit(inputData_signif), form.lm=currMod, m=5, dots=FALSE, seed=29, legend.pos="topleft", printit=FALSE));
mean_squared_error <- attr(cvResults, 'ms')
## 将需要的值放入Final_Ouput中
currOutput <- data.frame(formula=form, R_Sq=r_sq, Adj_RSq=adj_r_sq, AIC=aic, BIC=bic, Model.pValue= model_p, F.Statistic=f[1], training.mape=training_mape, predicted.mape=predicted_mape, training.minmax.accuracy = training_min_max_accuracy, predicted.minmax.accuracy=predicted_min_max_accuracy, influential.obs = influential_obs_rownums, k_fold_ms=mean_squared_error)
Final_Output <- rbind(Final_Output, currOutput)
## 打印输出
names(actual_fitted) <- c("actuals", "predicted")
actuals_predicted_all <- rbind(actual_fitted, actual_predicteds)
print (currSumm)
print (vif(currMod))
print (actuals_predicteds_predictors <- cbind(actuals_predicted_all, na.omit(inputData_signif)[, preds]))
}
write.csv(Final_Output, "Final_Regression_Output.csv", row.names=F) # 输出结果的CSV文件
Final_Regression_Output是包含所有模型的诊断参数的最终输出文件。在下表中是其中一个例子
| 参数 | 值 |
|---|---|
| 式: | response ~ Humidity + Visibility + Month |
| r.squared: | 53.04% |
| adj.r.squared: | 48.97% |
| AIC: | 1070.03 |
| BIC: | 1116.53 |
| Model.pValue: | 7.04E-19 |
| F.Statistic: | 13.03 |
| training.mape: | 62.51% |
| predicted.mape: | 73.71% |
| training.minmax.accuracy: | 66.84% |
| predicted.minmax.accuracy: | 61.00% |
| influential.obs(行号): | 11 13 24 34 41 80 87 89 106 157 |
| k_fold_ms(交叉验证均方误差): | 36.34% |
选择最佳模型并进行最终预测
一旦我们拥有模型,诊断和性能准确性,研究人员就可以选择适合特定业务问题的最佳模型。选择良好回归模型时的一般惯例如下:
| AIC / BIC:尽可能低 |
| MAPE和Min-Max准确度:尽可能高,接近100% |
| k-Fold交叉验证均方误差:越低越好。 |
| R-Sq和Adj R-Sq:越高越好。 |
在所有条件相同的情况下,如果有两个具有大致相同的预测精度的模型,则总是偏向于更简单的模型。
基于Final_Output中的结果,我们可以推断第10行中的模型几乎在每个参数中都表现良好,特别是预测的最小 - 最大精度和预测准确度。因此选择它作为最佳模型。
如何解释交叉验证图表?
由于我们正在执行5折交叉验证(在CVlm函数中m = 5),图表中有5种颜色和符号,每种颜色和符号就是一次折叠。图表中的5条虚线就是相应折叠的最佳拟合线。在交叉验证方法中,数据会被随机分成n(= 5)个折叠。通过将5个部分中的一个作为测试集,将剩余的4个部分构建为回归模型作为训练数据,然后该模型用于预测剩下的测试集。这是针对5个部分中的每个部分完成的,然后,实际值(图表中的较大符号)和预测变量(靠近线的较小符号)与最佳拟合线一起绘制在同一图表上。
一个非常好的模型,将使所有这些线彼此平行,并且更大的符号更接近线。
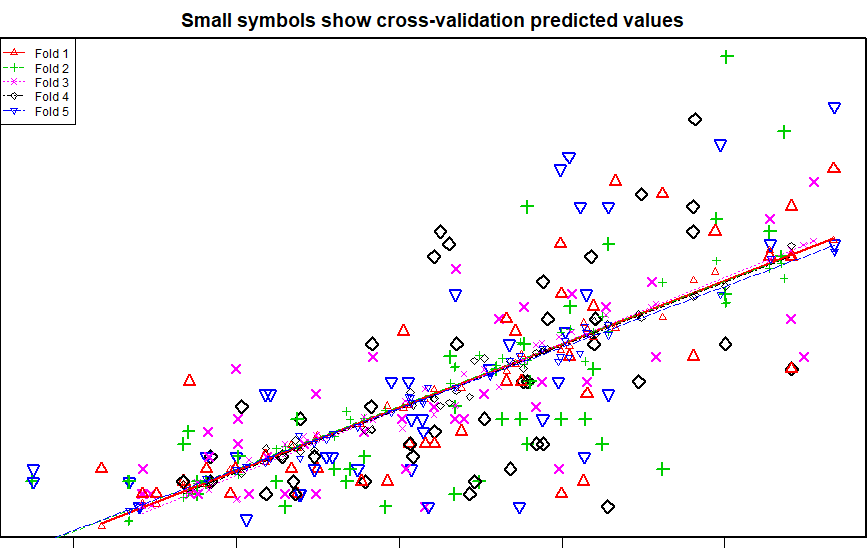
交叉验证图表
现在让我们从Final_Regression_Output.csv中选择第10行中的最佳模型,并生成预测和统计数据。
rownum=10
preds <- na.omit(combos_matrix[rownum, ])
form <- paste ("response ~ ", paste (preds, collapse=" + "), sep="")
currMod <- lm(as.formula(form), data=inputData_signif_training)
currSumm <- summary(currMod)
vif(currMod)
# 计算相对重要性
rel_importance <- try(calc.relimp(currMod, rela = T), silent=TRUE)
print (rel_importance$lmg) # print relative importance
predicted <- predict(currMod, inputData_signif_test) # predict on test data
actuals <- inputData_signif_test$response # actuals on test data
actuals_predicted_test <- data.frame(actuals=actuals, predicted=predicted)
actuals_predicted_test$min_max_accuracy <- apply(actuals_predicted_test, 1, min)/apply(actuals_predicted_test, 1, max) # calc min_max accuracy
print (actuals_predicted_test)
influence.measures(currMod) # 得到有影响的观察值
Call:
lm(formula = as.formula(form), data = inputData_signif_training)
Residuals:
Min 1Q Median 3Q Max
-13.9639 -4.5190 -0.2881 3.6861 21.9009
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.5940760 1.7929733 4.793 3.71e-06 ***
Humidity 0.1392783 0.0248104 5.614 8.48e-08 ***
Inversion_base_height -0.0020292 0.0002754 -7.368 8.54e-12 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.433 on 161 degrees of freedom
Multiple R-squared: 0.4095, Adjusted R-squared: 0.4022
F-statistic: 55.84 on 2 and 161 DF, p-value: < 2.2e-16
获得有影响力的观察值
cutoff <- 4/(nrow(inputData_signif_training)-length(currMod$coefficients)-2)
plot (currMod, which=4, cook.levels=cutoff)
abline (h=cutoff, lty=2, col="red")
influencePlot (currMod)
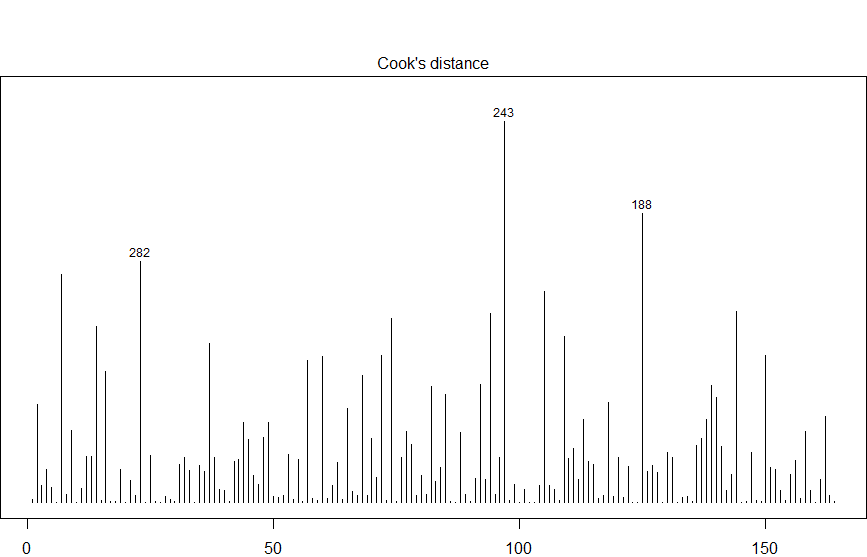
有影响力的观察值
鸡腿吃不腻
1楼 - 6 年,5 月 之前
有木有wifi有木有wifi,还是五毛耐用的!