数据挖掘的应用场景
首先是聚类分析,就是将不同的对象,根据其变量特征的分布自然地分成不同的类别。此外是分类模型,这是针对已知的类别,构建出分类的模型,通过分类的模型来探求其他未分类对象的类别。第三是预测估计,集根据对象的连续数据因变量,通过围绕已知的维度,构建出预测因变量的模型,从而对因变量未知的对象进行估计。最后是关联分析,即通过探求数据对象之间的相关关系,来发现对象之间的联系,在关联分析中,更多是以对象之间的关系作为输出。
聚类分析
聚类分析是一种无监督学习的数据挖掘方法,其目的是基于对象之间的特征,自然地将变量划分为不同的类别。在聚类分析中,基本的思想就是根据对象不同特征变量,计算变量之间的距离,距离理得越近,就越有可能被划为一类,离得越远,就越有可能被划分到不同的类别中去。

聚类分析基本思想
例如在坐标系中,B距离A的距离远远小于,B到C的距离,因此,AB更容易划分为一类,而BC更容易为不同的类别。通常来说,一个对象距离同类的距离是最近的,都小于其他类别中对象的距离。
在聚类分析中,有两种常用的方法,一种是K-means聚类,一种是层次聚类。

K-means聚类VS层次聚类
在K-means聚类中,是预先规定出要产生多少个类别的数量,再根据类别数量自动聚成相应的类。对K-means而言,首先是随机产生于类别数相同的初始点,然后判断每个点与初始点的距离,每个点选择最近的一个初始点,作为其类别。当类别产生后,在计算各个类别的中心点,然后计算每个点到中心点的距离,并根据距离再次选择类别。当新类别产生后,再次根据中心点重复选择类别的过程,直到中心点的变化不再明显。最终根据中心点产生的类别,就是聚类的结果。正如图中所示,一组对象中需要生成三个类别,各个类别之间都自然聚焦在一起。
在层次聚类中,不需要规定出类别的数量,最终聚类的数量可以根据人为要求进行划分。对层次聚类,首先每个对象都是单独的类别,通过比较两两之间距离,首先把距离最小的两个对象聚成一类。接着把距离次小的聚成一类,然后就是不断重复按距离最小的原则,不断聚成一类的过程,直到所有对象都被聚成一类。在层次聚类中,可以以一张树状图来表示聚类的过程,如果要讲对象分类的话,就可以从根节点触发,按照树状图的分叉情况,划分出不同的类别来。在图中,把一组对象分成了三个类别,可见这三个类别就是构成了树状图最开始的三个分支。
聚类分析的过程,和分桔子其实很很像,人们通常都把特征相同的桔子分成一类,聚类分析中,也是同样的方式。
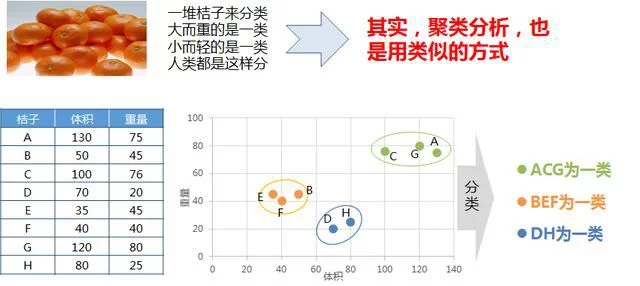
聚类分析案例
正如在这个例子中,有A-H的8个桔子,对每个桔子而言有提体积和变量两个变量。通过将各个桔子投射到重量和体积构成的坐标系中,可以发现BEF距离很近,ACG距离很近,而DH距离很近。如果聚成3类的话,可以是ACG、BEF,DH各为一类。如果是聚成两类,BEFDH与ACG相对更近,因此可以是ACG为一类,而BEFDH为另外一类
分类模型
分类模型通常是通过监督学习产生的,根据已知的对象的类别和其具体特征特征的数据,通过训练从而产生由特征判断类别的规则。在分类模型中,规则的输出就是具体的类别。

分类模型基本思想
分类模型的规则产生的过程中,类别判别的原则与训练集中各特征变量的分布息息相关,通常就是在对比各个类别下特征变量的互相关系,而划分出相关的规则,这个过程遵循的原则就是尽可能让输出的类别与实际的类别保持一致。
当前,不管在学术研究领域还是业务应用领域都有大量的分类模型,通常来说,决策树和朴素贝叶斯是非常普遍的分类模型算法,这两个算法在一些文献中也被列为十大数据挖掘算法。

决策树VS朴素贝叶斯
决策树的规则生成算法是将对象按照相关的特诊变量进行依次拆分,在拆分中不断迭代条件,最终划分为最终的类别。决策树的划分过程,就像是一个树一样,从根节点触发,依次开支散叶,最终形成分类准则。
在图中,首先就按照年龄进行分支,直接将所有对象分成了三堆,其中年龄在31-40岁的被划定为购买类,另外的两堆对象,还需要继续进行分支。对年龄小于30岁,按照是否为学生进行分支,其中是学生的被判定为购买类,不是学生的被判定为不买类。同样对年龄大于40岁,按照信用等级进行分类,信用等级高的被判定为不买类,信息等级低的被判定为购买类。就这样,任何一个对象,都可以根据条件达成的情况,最终到达购买或者不买的节点,完成分类过程。
朴素贝叶斯的规则生成算法相对决策树而言,就没有这么直观了,其依赖于概率中的贝叶斯公式。由公式P(AB)=P(A/B)×P(B)=P(B/A)×P(A)得来的后验概率公式P(A/B)=P(B/A)×P(A)/P(B),其中A类别,B表示条件即特征变量。P(A/B)表示在特定条件下该类别的概率,P(B/A)表示在特定类别下该条件的分布概率,P(A)表示已知的特定分类的概率,而P(B)表示已知的特定条件的概率。
在算法中,P(B/A)、P(A)、P(B)都通过训练集能够得到,再加上在条件一定时,P(B)是恒定的,同时每个条件互相独立,根据概率公式,P(类别/总条件)是P(类别)和所有P(条件/类别)的乘积。因此在朴素贝叶斯中,最大的P(类别/总条件)对应的类别,就是被划分的类别。
最近这几年,网上总有要远离女司机的段子,在网友心中女司机简直如洪水猛兽一般,这种说法一方面来自于个别事例的传播,另外一方面也来自于女司机在低速驾驶时对他人的困扰造成的误解。其实,对于女司机是不是应该害怕的问题,就可以用分类模型的解决。

用分类模型解决女司机问题
已知道路上的车辆中的分布如下,会发生的事故的概率有0.11,而是安全的概率有0.89,车辆的分布就是对事件的原始分类分布。同时,对发生条件的分布如下,发生事故时,男司机概率为0.9,女司机概率为0.1,在安全情况下时,男司机概率为0.2,女司机概率为0.8。
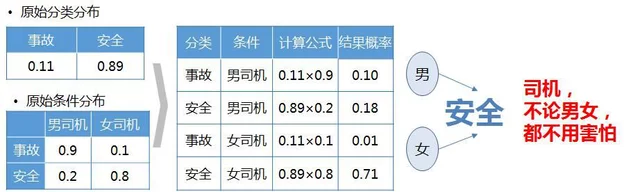
分类模型案例计算流程
那么根据贝叶斯公式,可以知道,当遇到男司机时,发生事故的概率为0.1,而女司机是0.01,两者的事故的概率都很低。对男女司机而言,其发生事故的概率都低于安全的概率,因此在职考虑性别的情况下,所有司机都是被分为安全类别,尤其是女司机,安全的概率远远大于事故。因此不能简单的通过司机的性别,就做出是否危险的判别,尤其是遇到女司机。
关联分析
关联分析模型常用于揭示事件之间的关系,是通过无监督学习的方式,产生的输出事件之间发生关系的规则。关联分析最开始在零售领域常常用到,比如可以提供买了方便面时很多情况都会买火腿肠的关系,因此在某些情况下,关联分析又被称为购物篮分析。

关联分析基本思想
在购物篮分析中,其核心思想就是对比单个事件发生的概率,和多个事件同时发生的概率的情况,如果同时发生的概率与单独发生的概率相近,则可以考虑发生了一个事件后,很有可能会存在同时发生另外一个事件的情况。
有事件X和事件Y,以及XY同时发生的概率,在购物篮分析中,支持度是XY同时发生的概率,置信度是当X发生了,Y也发生的条件概率。

关联分析算法
如果在规则中,两个事件的支持度和置信度都达到了制定的阈值,则可以认为这两个事件具有强关联的关系。关联分析正是体现了这种强关系。在强关系中,还有提升度来确认这种强关系的力度,提升度是指,当X出现同时出现Y的概率,与Y总体出现的概率之比,即X对Y的置信度与Y发生概率的比值,通常来说提升度都是大于1的,提升度越大,说明强关系力度越大。
在关联分析中,强关系存在两种情况,这种情况具有不同的时间上的考虑,第一种是序列关系,即事情顺次发生,比如购买了A了以后又继续购买B,另外一种是同时关联,即事件同时发生,比如买了A的同时也买了B。
啤酒和尿布是关联分析中的经典案例,尽管最近出现了这个只是编造的案例而已,然而去仍然能体现出关联分析的价值出来。

在啤酒和尿布中发现关联分析的价值
啤酒和尿布,两个看起来不无相关的物品,却可以通过关联分析,找出进行同时销售的机会出来,其背后的原理就是发现了,啤酒和尿布之间的强关联关系。

关联分析案例计算过程
假设有尿布,啤酒,零食,水果和香烟的五种商品,同时也知道了各个商品购买的清单,根据清单可以提取单个产品的频数和其对应的概率,以及产品之间两两组合带来频数和概率。根据支持度和置信度的计算公式,可以得到,每个产品组合的支持度,以及置信度。设置强关联最小支出度阈值以及最小置信度阈值都为0.5时,啤酒对尿布达到了强关联的阈值,因此啤酒对尿布这对组合可以认为具有强关联,因此在购买啤酒时推荐购买尿布,能够增加尿布的销量。
预测估计
预测估计的规则,是用来输出连续的数值,即通过预测估计的规则,模型输出的是系列的数值,这些数值可以进行加减乘除的一系列计算。
预测估计基本思想
预测估计的规则通常以一个公式存在,这个公式可以体现出要输出的因变量Y与特征变量X的关系,最简单的来说,像一条在坐标系反应Y和X关系的直线一样,知道了X是多少的情况,就可以根据线性关系,输出对应的Y。这种思路正式用于生成回归方程,因此有的时候预测估计也被称为是回归。
在预测估计中,首先是对比训练集中要输出的因变量Y和特征变量X的关系,通常来说,X不只有一个,而是有X1,X2,X3,Xn等多个,在这种情况下,通过学习X1到Xn与Y的数学关系,从而产生出能够基于X1到XN预测出Y的规则。如果规则通过验证集的验证,就可以在实习情况中与预测要输出的因变量Y。
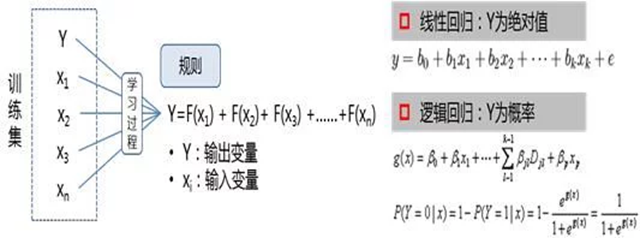
预测估计算法
预测估计的输出变量可以是绝对值也可以是相对值,在输出绝对值的情况下,线性回归是常用的模型,即生成一条关于Y与X1到Xn的直线方程,用来预测Y。在输出相对值得情况,逻辑回归是常用的模型。在逻辑回归中,输出的Y是概率,在规则中通过拟合X的直线,产生出一个结果,再将直线输出结果进行指数化转换,最终结果就是的Y,即事件发生概率。
下面是一个用预测估计的模型来预测谁可以得奖的例子,在这个例子中,并不是直接用模型预测得奖的人员,而是通过对过去得奖的人员的数据进行学习,从而得出计算得奖概率的规则,并通过学习到的规则,根据本次所有人的表现的数据,来预测各自的将概率。

用预测估计知道得奖概率
在这个例子中,共有7个变量,其中过去得奖是作为0-1因变量存在,1表示得奖,0表示未得奖。在自变量中有另外6个变量。通过对历史的数据的学习,能够得到logit的计算公式,并根据概率换算的公式,得到概率的公式。
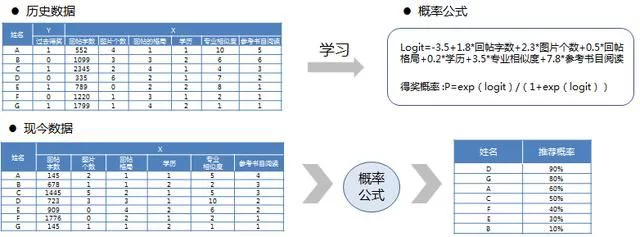
再进一步地,取得当前数据后,根据概率公式,得到每个人为的得奖概率,概率最大的即为最可能得奖的人。
挖掘思维总结
在挖掘思维是与数据挖掘相关,相比前面几种思维而言,挖掘思维似乎要晦涩难懂一些,毕竟数据挖掘涉及的已经不局限于简单的数学,而且还扩充到了计算机科学层面。这里设置挖掘思维,其目的就是在解答,当数据量实在太大时,维度实在太多时,应该如何来处理的问题。
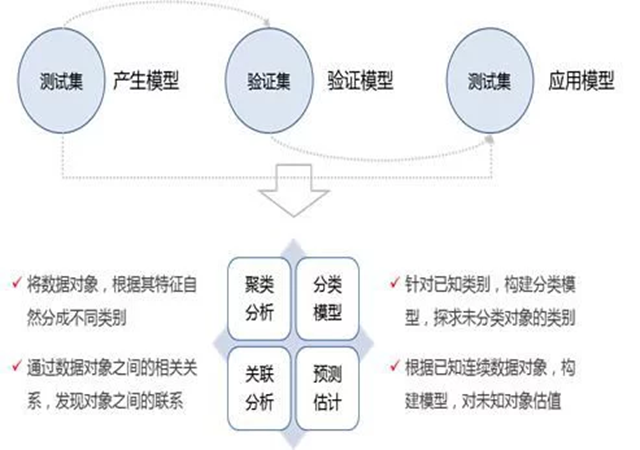
挖掘思维总结
数据挖掘的实质,其实还是为了得到一个模型,产生结果。当数据需要特别复杂的计算过程时,数据挖掘就能够产生作用了。数据挖掘通常通过已知输出的结果的数据中作为训练集产生出模型,再用另外一部分知道已知输出结果的数据作为验证集来验证模型的可信程度,通过验证后,再用到测试集中去取得实际的效果。
数据挖掘分为四种类型,就像前面所述,四种类型分别是聚类分析、分类模型、关联分析和预测估计。聚类分析是将数据对象,根据其特征自然分成不同类别。分类模型是针对已知类别,构建分类模型,探求未分类对象的类别。关联分析是通过数据对象之间的相关关系,发现对象之间的联系。预测估计就是根据已知连续数据对象,构建模型,对未知对象估值。
举一个简单的例子,知道一个班之间学生平时作业的情况,将学生自动分成若干类别,就是聚类分析,这些有可能是学霸型,学渣型,还有可能是偏科型,到底类别怎么样,事前都不知道,要聚类以后才知道。已知一部分学生的类别,而不知道另外一部分学生,就用分类模型的方式得出另外一些学生的类别。知道一些学生挂语文的同时还容易挂哪些学科,就是关联分析。从学生平时作业来预测他们期末考试分数就是预测估计。