当我们实际构建模型时会发现,建一个有效统计显着的回归模型可能是一项艰巨的任务,特别是我们不熟悉数据或者问题时,面对多个选择时往往会陷入迷茫。 这一节就让我们灵活地构建所有可选的统计有效模型,并查看其预测准确性,对随机样本进行交叉验证,最后选择最适合您情况的最佳诊断参数。 由于R语言在统计分析和算法方法提供了强大简洁的支持,在实际情况中,我们会结合两者的优点来寻找,构建,分析和选择最佳的线性回归模型。以下的分析框架试图在稳健算法与调查方法之间取得平衡。
由于R语言在统计分析和算法方法提供了强大简洁的支持,在实际情况中,我们会结合两者的优点来寻找,构建,分析和选择最佳的线性回归模型。以下的分析框架试图在稳健算法与调查方法之间取得平衡。
如果需要学习统计、回归建模的基础知识,请查看R教程-13:线性回归模型等前面的教程。
问题描述
本次实验数据来自mlbench软件包的“ozone”数据,该数据包含1976年收集的洛杉矶臭氧污染数据。它有366行和13个变量,由我们来确定哪些可用变量最适合预测臭氧读数。所以总的来说,本次分析的目的是使用线性回归模型准确预测“每日最大一小时平均臭氧读数”(daily maximum one-hour average ozone reading)。
我们将通过将数据拆分为80%训练集和20%的测试集来确保预测效果,根据20%验证样本的实际预测臭氧读数得到的预测精度将被用为解决该问题的重要参数之一。
开始:加载包并准备输入数据
加载包
library(e1071) # 偏态分析用的
library(PerformanceAnalytics) # 画相关图的
library(Hmisc) # 缺失值处理的包
library(corrplot) # 也是相关图的包
library(party) # 用来选择最佳参数
library(Boruta) # 决定参数是否重要
library(caret) # boxcox转换
library(car) # Vif
library(DMwR) # K近邻补值
library(mlbench) # Ozone 数据
library(DAAG) # 用于交叉验证
library(relaimpo) # 用来找相关的预测重要性
准备输入数据
data (Ozone, package="mlbench") # 导入实验数据
inputData <- Ozone
# 分配列名
names(inputData) <- c("Month", "Day_of_month", "Day_of_week", "ozone_reading", "pressure_height", "Wind_speed", "Humidity", "Temperature_Sandburg", "Temperature_ElMonte", "Inversion_base_height", "Pressure_gradient", "Inversion_temperature", "Visibility")
#将连续和分类变量进行处理
#将所有连续变量放在inputData_cont中
inputData_cont <- inputData[, c("pressure_height", "Wind_speed", "Humidity", "Temperature_Sandburg", "Temperature_ElMonte", "Inversion_base_height", "Pressure_gradient", "Inversion_temperature", "Visibility")]
# 将所有分类变量放在inputData_cat中
inputData_cat <- inputData[, c("Month", "Day_of_month", "Day_of_week")]
# 创建对应的数据集
inputData_response <- data.frame(ozone_reading=inputData[, "ozone_reading"])
response_name <- "ozone_reading" # 预测变量的列名
response <- inputData[, response_name] # 预测数据
 臭氧数据
臭氧数据
创建派生变量
在继续进行探索性分析之前,最好从预测变量中导出尽可能多的新变量,在这一步创建新变量是为了方便后续的分析进行统计验证并进行筛选。
| 创建派生变量的思路 | |
|---|---|
| 组合 | 新变量是少数原始原始变量的组合(+ / *) |
| 聚合 | 将变量聚合到某个级别。例如:过去12个月的销售额,某个就业类别的平均工资等。 |
| 转换 | 将变量转换为log,cube等。下面将讨论Box-Cox转换。 |
| 时间变换 | 线季节性,假期指标,月份,周指标,星期几等。 |
| 指标 | 公开(或可购买)可用数据来源的相关经济指标 |
这是一个挑战:你能为“臭氧”数据集想出一个新的派生变量吗?如果成功,请将该变量附加到输入数据并继续进行分析。在此分析结束时,看看是否可以构建比我们更好的预测模型变量。
探索性分析
# 生成图,密度图、散点图、箱线图
for (k in names(inputData_cont)){
png(file=paste(k,"_dens_scatter_box" ,".png", sep=""), width=900, height=550)
x <- as.numeric (inputData_cont[, k])
Skewness <- round(skewness(x), 2) # calc skewness
dens <- density(x, na.rm=T) # density func
par(mfrow=c(1, 3)) # setup plot-area in 3 columns
# 密度图
plot(dens, type="l", col="red", ylab="Frequency", xlab = k, main = paste(k, ": Density Plot"), sub=paste("Skewness: ", Skewness))
polygon(dens, col="red")
# 散点图
plot(x, response, col="blue", ylab="Response", xlab = k, main = paste(k, ": Scatterplot"), pch=20)
abline(response ~ x)
# 箱线图
boxplot(x, main=paste(k, ": Box Plot"), sub=paste("Outliers: ", paste(boxplot.stats(x)$out, collapse=" ")))
dev.off()
}

压力高度密度散点图
上面的代码循环画了连续变量的密度图、散点图和箱形图,并将其存储在工作目录中。 密度图最好有与图表区域中心对齐的钟形曲线。 散点图显示预测变量和响应之间是否存在潜在的线性关系,而箱形图显示变量中的任何异常值(在这种情况下,点将出现在顶部和底部线(IQR)之外)。
离群点分析
方法1:删除异常值(不推荐)
x <- x[!x %in% boxplot.stats(x)$out] # NOT run!
方法2:用NA替换异常值,稍后在缺失值处理期间填写。
replace_outlier_with_missing <- function(x, na.rm = TRUE, ...) {
qnt <- quantile(x, probs=c(.25, .75), na.rm = na.rm, ...) # 算25% 75%值
H <- 1.5 * IQR(x, na.rm = na.rm) # 算界限值
y <- x
y[x < (qnt[1] - H)] <- NA # 替换小于值
y[x > (qnt[2] + H)] <- NA # 替换大于值
y # 返回y
}
inputData_cont <- as.data.frame (sapply(inputData_cont, replace_outlier_with_missing)) # 引用我们的函数
使用异常值校正部分重新组合inputdata
inputData <- cbind(inputData_response, inputData_cont, inputData_cat)
缺失值处理
处理缺失值的方法
消除变量:如果特定变量的缺失值超过30%,建议考虑完全删除该变量。
消除观察结果:如果在数据集中散布了缺失值,并且样本中有大量观察结果,则可以选择删除缺少值的观察结果。执行此操作后,如果发现丢失的样本量超过30%,则可能需要查找导致缺失值最多的任何特定变量。
估算:也可以利用原本的数据来估算缺失值。
| 估算方法 |
|---|
| 平均值:用平均值替换 |
| 中位数:替换为中位数 |
| 中间值:替换为(最大值+最小值)/ 2 |
| 众数:最常见的值 |
| 基于插补:基于对变量的函数插值。 |
| 基于分布:识别变量的分布,以及使用该分布参数估计。 |
| 预测缺失值:基于在回归模型中将缺失视为因变量 |
| k近邻:基于发现有缺失值的观察最接近特征的观察,通过最近邻居法 |
应用缺失值处理
方法1:用均值替换缺失值
inputdata_cont_matrix <- sapply(inputData_cont, FUN=function(x){impute(x, mean)})
inputdata_cont <- as.data.frame(inputdata_cont_matrix)
方法2:通过使用基于回归模型的方法
将其建模为因变量来预测缺失值使用均值替换所有缺失值,但响应变量除外。使用变量构建模型,需要将缺失值处理作为响应变量,而其余变量可以用作预测变量。这种方法在Julian J Faraways的书P.158中讨论过。
方法3:k-最近邻插补法
# 对所有缺失值处理
if( anyNA(inputData)) {
inputData[, !names(inputData) %in% response_name] <- knnImputation(inputData[, !names(inputData) %in% response_name])
}
相关分析和总结
相关图是响应和预测变量的所有组合之间的相关性的图形表示。研究者可以选择基于预先确定的截止值来选择与响应具有高相关性的变量。但是我们在这里不进行过滤,因为即使相关性较低的变量有“较低”的重要性,但它们可能在回归模型中也是重要且有价值的。
par (mfrow=c(1,1))
inputData_response_cont_noNA <- na.omit(cbind(inputData_response, inputData_cont)) # 移除NA值
chart.Correlation(inputData_response_cont_noNA, histogram=TRUE, pch=19) # 画相关性图
corrplot(cor(inputData_response_cont_noNA), method="circle", is.corr=TRUE)
# 获取并存储总结文件
sapply(inputData, summary)

Correlogram - 蓝色圆圈显示正相关,红色圆圈显示负面影响。圆圈越大,相关性越高。
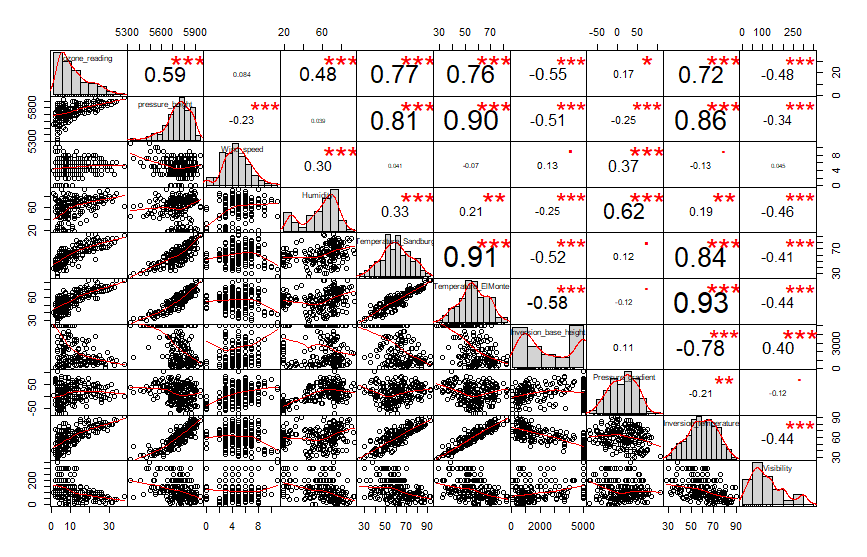
具有密度,散点图和显着相关值的Correlogram。
连续变量的Box Cox变换
在执行异常值处理时,我们预期变量的偏差会得到改善,不过效果可能不会,这个时候响应变量的box-cox变换可能更可取,因为该种方法减少偏斜并使其更接近正态分布。变量变换后,其排序顺序保持不变。
为什么高度偏斜的非正常响应变量很重要?
因为对于响应的长尾区域,往往存在较大的方差。这也意味着在解释响应变量的较大方差的部分时,预期更多预测因子具有更强的效果,从而会产生偏差,这会导致虚假模型的估计值。
因此,如果在处理异常值后偏斜没有改善,则考虑执行box-cox变换,尤其是当k-fold交叉验证显示不一致的结果时。请注意,并非必须对所有倾斜的变量都应用box-cox变换,而是根据我们的分析来处理。
默认情况下,响应变量中的box-cox变换就足够了,但是在这里,我们选择将它应用于偏差> 1的变量。
skewness(inputData_response, na.rm=T) # 0.878864
# 转换
boxcoxTransformedVars <- character(0)
for (colname in colnames(inputData_cont[, -1])) {
x <- inputData_cont[, colname]
if(abs(skewness(x, na.rm=T)) > 1){ # 检测偏度
boxcoxMod <- BoxCoxTrans(x)
boxcoxTransformedVars <<- c(boxcoxTransformedVars, colname)
inputData_cont[, colname] <- predict(boxcoxMod, x)
}
}