我们现在有多维的数据,还有一个想要预测出规律的响应变量,如何挑出最重要的预测变量是一门十分关键有用的技术,这一节就来介绍如何用R语言做到这招!
数据准备
为了说明各种方法,我们将使用'mlbench'包中的'臭氧'数据。# Data Preparation
#准备数据!
library(mlbench)
data(Ozone, package="mlbench")
inputData <- Ozone
names(inputData) <- c("Month", "Day_of_month", "Day_of_week", "ozone_reading",
"pressure_height", "Wind_speed", "Humidity", "Temperature_Sandburg",
"Temperature_ElMonte", "Inversion_base_height", "Pressure_gradient",
"Inversion_temperature", "Visibility")
填补缺失值
#用k邻接法去填充缺失值
library(DMwR)
inputData <- knnImputation(inputData)
隔离连续和分类变量
#将连续变量都放到inputData_cont
inputData_cont <- inputData[, c("pressure_height", "Wind_speed", "Humidity", "Temperature_Sandburg", "Temperature_ElMonte", "Inversion_base_height",
"Pressure_gradient", "Inversion_temperature", "Visibility")]
#将分类变量放到inputData_cat
inputData_cat <- inputData[, c("Month", "Day_of_month", "Day_of_week")]
#选择我们要预测的响应变量ozone reading值!
inputData_response <- data.frame(ozone_reading=inputData[, "ozone_reading"]) #
response_name <- "ozone_reading"#响应变量名字
response <- inputData[, response_name] #响应变量的数据
1.随机森林方法
随机森林可以非常有效地找到一组最能解释响应变量方差的预测变量。
library(party)
#做一个随机森林模型
cf1<-cforest(ozone_reading~.,data=inputData,control=cforest_unbiased(mtry=2,ntree=50))
varimp(cf1)#根据平均下降准确率得到因素们的重要性
varimp(cf1, conditional=TRUE) # conditional=TRUE这个参数是为了调整掉因素之间的相关
varimpAUC(cf1) #基于分类的不平衡做更强的解释处理
#我们的结果
# Month
# 3.07240463
#
# Day_of_month
# 0.05763824
#
# Day_of_week
# 0.23705288
#
# pressure_height
# 7.07962903
#
# Wind_speed
# 0.18803550
#
# Humidity
# 3.48513051
#
# Temperature_Sandburg
# 11.15242224
#
# Temperature_ElMonte
# 13.76939819
#
# Inversion_base_height
# 3.97817073
#
# Pressure_gradient
# 2.34617215
#
# Inversion_temperature
# 7.88156535
#
# Visibility
# 2.43741341
2.相对重要性
使用relaimpo包里面的calc.relimp函数,根据线性回归模型的变量相对重要性来确认因素重要程度。
library(relaimpo)
lmMod <- lm(ozone_reading ~ . , data = inputData)#做一个线性模型
relImportance <- calc.relimp(lmMod, type = "lmg", rela = TRUE) #计算相对重要性#
sort(relImportance$lmg, decreasing=TRUE)#相对重要程度
## 我们的结果
# Temperature_ElMonte
# 0.184722438
# Temperature_Sandburg
# 0.164540381
# Month
# 0.163371978
# Inversion_temperature
# 0.137890248
# pressure_height
# 0.087594494
# Inversion_base_height
# 0.083696664
# Humidity
# 0.068573808
# Visibility
# 0.039202230
# Day_of_month
# 0.031248599
# Pressure_gradient
# 0.026557629
# Day_of_week
# 0.008371262
# Wind_speed
# 0.004230269
3. MARS方法
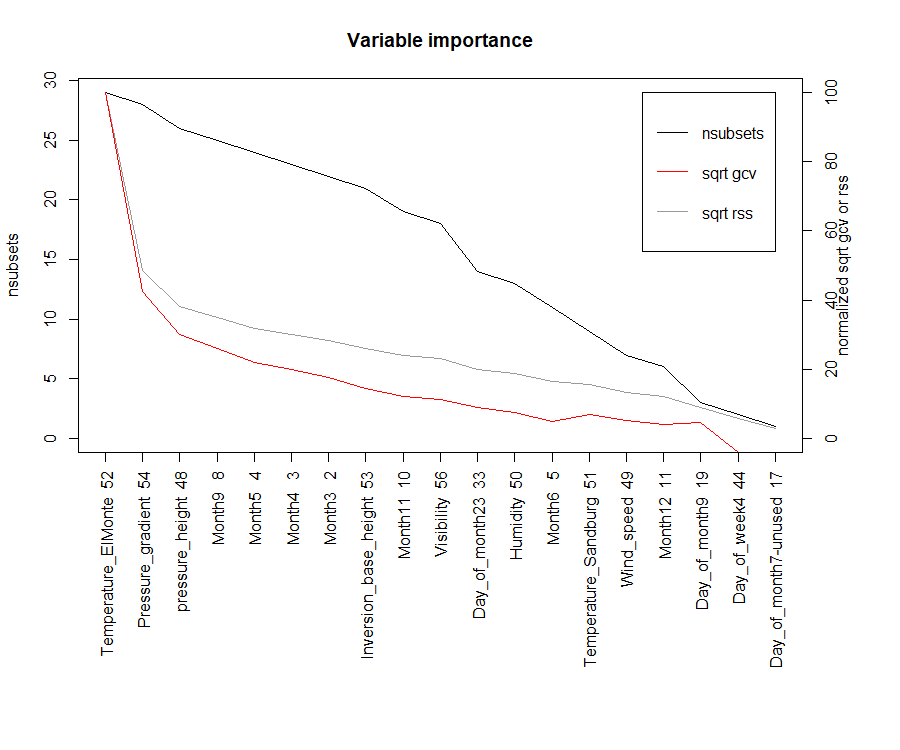
基于广义交叉验证(GCV)变量重要性,变量发生(nsubsets)和残差平方和(RSS)的子集的模型数目来确定因素的重要程度,用的是Earth包。
library(earth)
marsModel <- earth(ozone_reading ~ ., data=inputData)#建立一个gcv模型
ev <- evimp (marsModel)#估算重要程度
plot (ev)#做一下可视化
# ev
# nsubsets gcv rss
# Temperature_ElMonte 21 100.0 100.0
# Pressure_gradient 20 42.7 47.1
# pressure_height 18 30.7 36.3
# Month9 17 26.8 32.9
# Month5 16 22.6 29.3
# Month4 15 20.6 27.4
# Month3 14 18.7 25.6
# Visibility 13 15.4 23.0
# Month6 11 12.6 20.1
# Day_of_month7 9 10.9 17.9
# Month2 9 10.5 17.7
# Temperature_Sandburg 9 10.5 17.7
# Day_of_month21 6 6.7 13.5
# Day_of_month23 4 3.7 10.4
# Wind_speed 2 3.5 7.6
# Month11 1 2.8 5.5
4.逐步回归
如果我们的数据自变量因素比较多(> 15),则可以将inputData拆分为10个预测变量的块,逐步的去求出来因素的重要程度。
base.mod <- lm(ozone_reading ~ 1 , data= inputData) #基本模型
all.mod <- lm(ozone_reading ~ . , data= inputData) #全类模型,包含了所有因素
stepMod <- step(base.mod, scope = list(lower = base.mod, upper = all.mod), direction = "both", trace = 1, steps = 1000)#逐步的方法
shortlistedVars <- names(unlist(stepMod[[1]]))
shortlistedVars <- shortlistedVars[!shortlistedVars %in% "(Intercept)"]#对重要性的排序
#Selected Variables
#[1]“Temperature_Sandburg”“Month2”“Month3”“Month4”
#[5]“Month5”“Month6”“Month7”“Month8”
#[9]“Month9”“Month10”“Month11”“Month12”
#[13]“Temperature_ElMonte”“Humidity”“Pressure_gradient”“Visibility”
#[17]“Wind_speed”“pressure_height”
如果我们的因素特别多(100+),那我们可以将上述代码放在循环中,该循环将在连续的预测变量块上逐步运行。可以累积入围的变量以在每次迭代结束时进行进一步分析。
5. Boruta
Boruta方法可以决定一个因素是否重要。
library(Boruta)
boruta_output <- Boruta(response ~ ., data=na.omit(inputData), doTrace=2)#通过boruta方法确认重要与否
# Confirmed 10 attributes: Humidity, Inversion_base_height, Inversion_temperature, Month, Pressure_gradient and 5 more.
# Rejected 3 attributes: Day_of_month, Day_of_week, Wind_speed.
boruta_signif<- names(boruta_output$finalDecision[boruta_output$finalDecision %in% c("Confirmed", "Tentative")]) # 收集确认的和不确认的因素
# Confirmed variables
# [1] "Month" "ozone_reading" "pressure_height" "Humidity"
# [5] "Temperature_Sandburg" "Temperature_ElMonte" "Inversion_base_height" "Pressure_gradient"
# [9] "Inversion_temperature" "Visibility"
6.信息价值和证据权重
library(devtools)
install_github("tomasgreif/riv")
install_github("tomasgreif/woe")
library(woe)
library(riv)
iv_df <- iv.mult(german_data, y="gb", summary=TRUE, verbose=TRUE)
iv <- iv.mult(german_data, y="gb", summary=FALSE, verbose=TRUE)
# iv_df
# Variable InformationValue Bins ZeroBins Strength
# 1 ca_status 0.666011503 4 0 Very strong
# 2 credit_history 0.293233547 5 0 Strong
# 3 duration 0.259146834 5 0 Strong
# 4 credit_amount 0.207970035 5 0 Strong
# 5 savings 0.196009557 5 0 Average
# 6 purpose 0.169195066 10 0 Average
# 7 age 0.125210683 5 0 Average
# 8 property 0.112638262 4 0 Average
# 9 present_employment_since 0.086433631 5 0 Weak
# 10 housing 0.083293434 3 0 Weak
# 11 other_installment 0.057614542 3 0 Weak
# 12 status_sex 0.044670678 5 1 Weak
# 13 foreign_worker 0.043877412 2 0 Weak
# 14 other_debtors 0.032019322 3 0 Weak
# 15 installment_rate_income 0.023858552 2 0 Weak
# 16 existing_credits 0.010083557 2 0 Wery weak
# 17 job 0.008762766 4 0 Wery weak
# 18 telephone 0.006377605 2 0 Wery weak
# 19 liable_maintenance_people 0.000000000 1 0 Wery weak
# 20 present_residence_since 0.000000000 1 0 Wery weak
绘制信息值图
iv.plot.summary(iv_df)
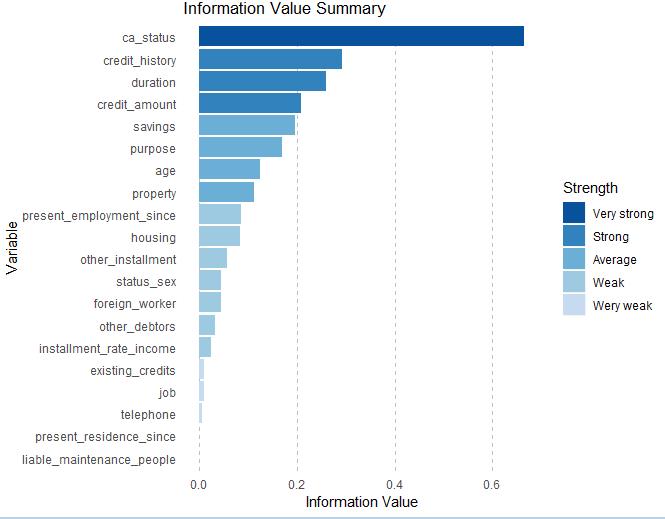
计算证据变量的权重
german_data_iv <- iv.replace.woe(german_data, iv, verbose=TRUE)
鹃儿
1楼 - 4 年,9 月 之前
我们现在有多维的数据,还有一个想要预测出规律的响应变量,如何挑出最重要的预测变量是一门十分关键有用的技术。