时序预测：利用R语言对游泳圈热度进行预测_数据挖掘

1. 思路

一些产品例如苹果、西瓜、游泳圈是明显有时序特点的，到了某些季度热度就会上升。了解这些时序规律，可以帮助我们在电商平台或短视频平台等提前进行广告投入，从而带来额外的收入。通过准确预测这些产品的热度，我们可以更有效地分配营销资源，提升销售额和品牌影响力。

2. 数据收集

热度信息可以通过百度等搜索平台的指数或趋势平台获得，例如https://index.baidu.com/v2/index.html#/。本文选择了游泳圈这个商品，并选取了美国的区域进行数据搜集（由于数据更好获得）。我们利用百度指数和Google Trends等工具，获取过去几年的游泳圈搜索热度数据，作为时序分析的基础数据。

3. 数据分析与预测

我们利用如下的脚本对热度趋势进行分析和预测，主要包含以下几个步骤：

3.0 数据结构与有效数据选取

首先，我们来导入必要的包。

library(xgboost)
library(tidymodels)
library(modeltime)
library(tidyverse)
library(lubridate)
library(timetk)
library(fpp3)

如果没有这个包的话，可以采用如下命令进行安装。

install.packages('xgboost')

然后来看数据的格式，从趋势平台下载数据后得如下数据，经过读取后格式如下

df<-read.csv("~/Downloads/swimring.csv")

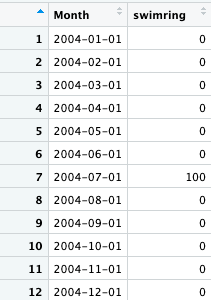
我们先将日期格式进行调整，然后选择明显有趋势规律的2007年以后的数据。

df <- df %>%
  mutate(Month = paste0(Month, "-01"))
df <- df %>%
  mutate(Month = as.Date(Month))
df<-df[df$Month>as.Date('2007-01-01'),]

3.1 基本可视化

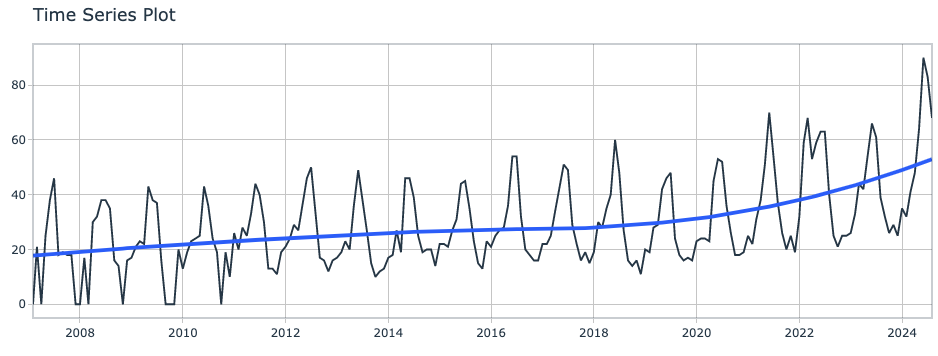
首先，通过绘制时间序列图，对游泳圈热度数据进行基本可视化分析。这样可以直观地观察热度随时间变化的总体趋势和波动情况，可以看到数据明显有按照年的时序性波动。

df %>% 
  timetk::plot_time_series(.date_var = Month,
                           .value = swimring)

3.2 季节性模式分析

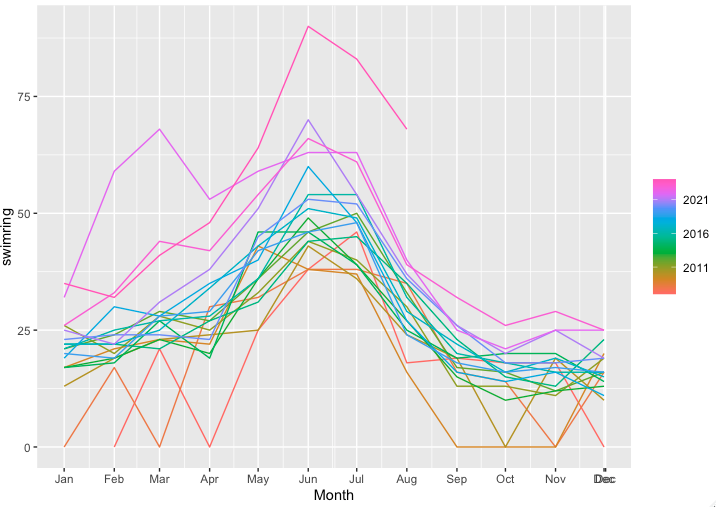
通过对数据进行季节性分解，识别出热度数据中的季节性模式。这一步有助于了解游泳圈热度在一年中不同时间段的变化规律。例如，游泳圈的热度可能在夏季7月8月达到峰值，而在冬季趋于低谷。

df <- tibble(df)

# Convert to tsibble type
df_ts <- df %>% 
  mutate(Month= yearmonth(Month)) %>%
  as_tsibble(index = Month)


# Seasonal Plot
df_ts %>% gg_season(swimring)

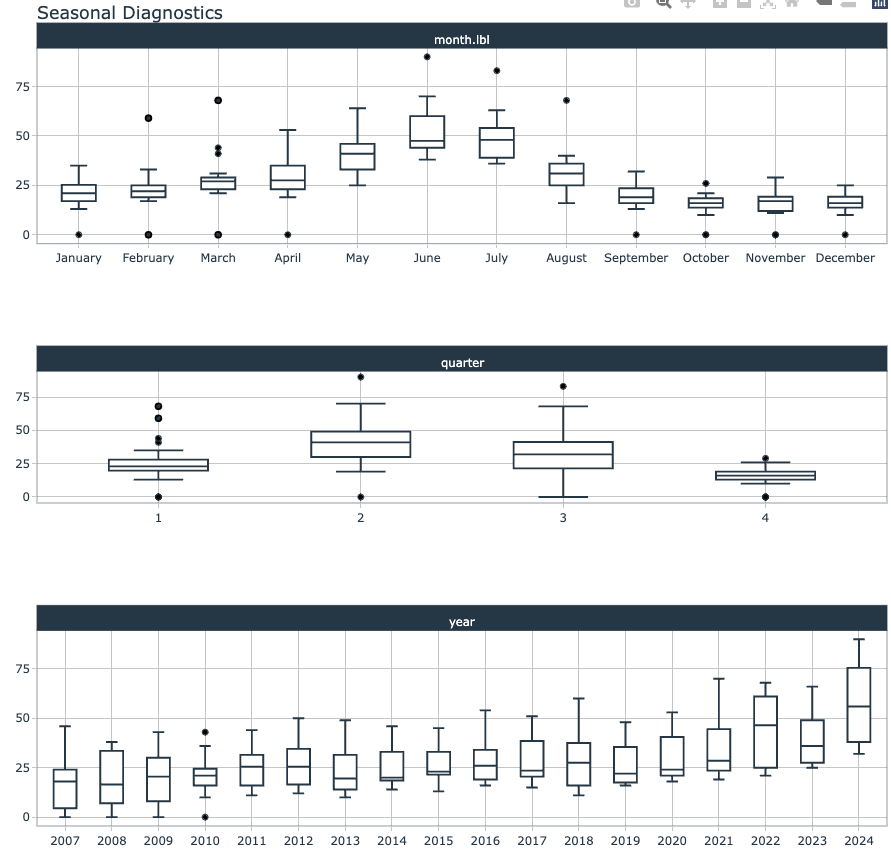
df %>% 
  timetk::plot_seasonal_diagnostics(.date_var = Month,
                                    .value = swimring)

3.3 异常数据识别

在时序数据中，有时会出现一些异常值。这些异常值可能是由于特定事件或数据错误引起的。通过异常数据识别，可以剔除或处理这些异常值，使得模型预测更加准确。

df %>% 
  timetk::plot_anomaly_diagnostics(.date_var = Month,
                                   .value = swimring)

这里我们可以看到22年2月 3月以及今年夏天的热度有一些异常。

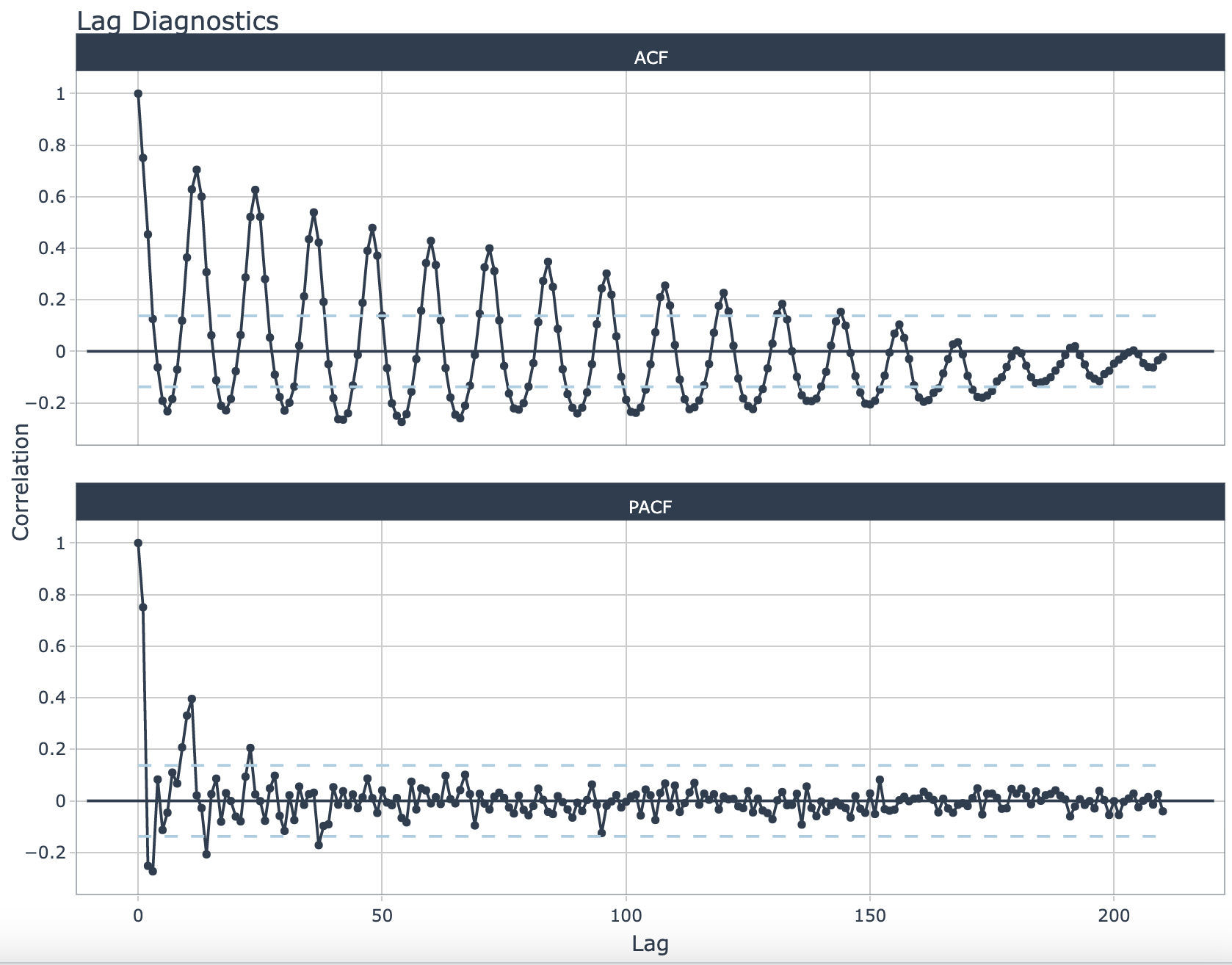
3.4 时序滞后性分析

时序数据中的某些特征可能具有滞后效应。通过滞后性分析，可以识别出热度数据中的滞后特征，从而改进模型的预测性能。

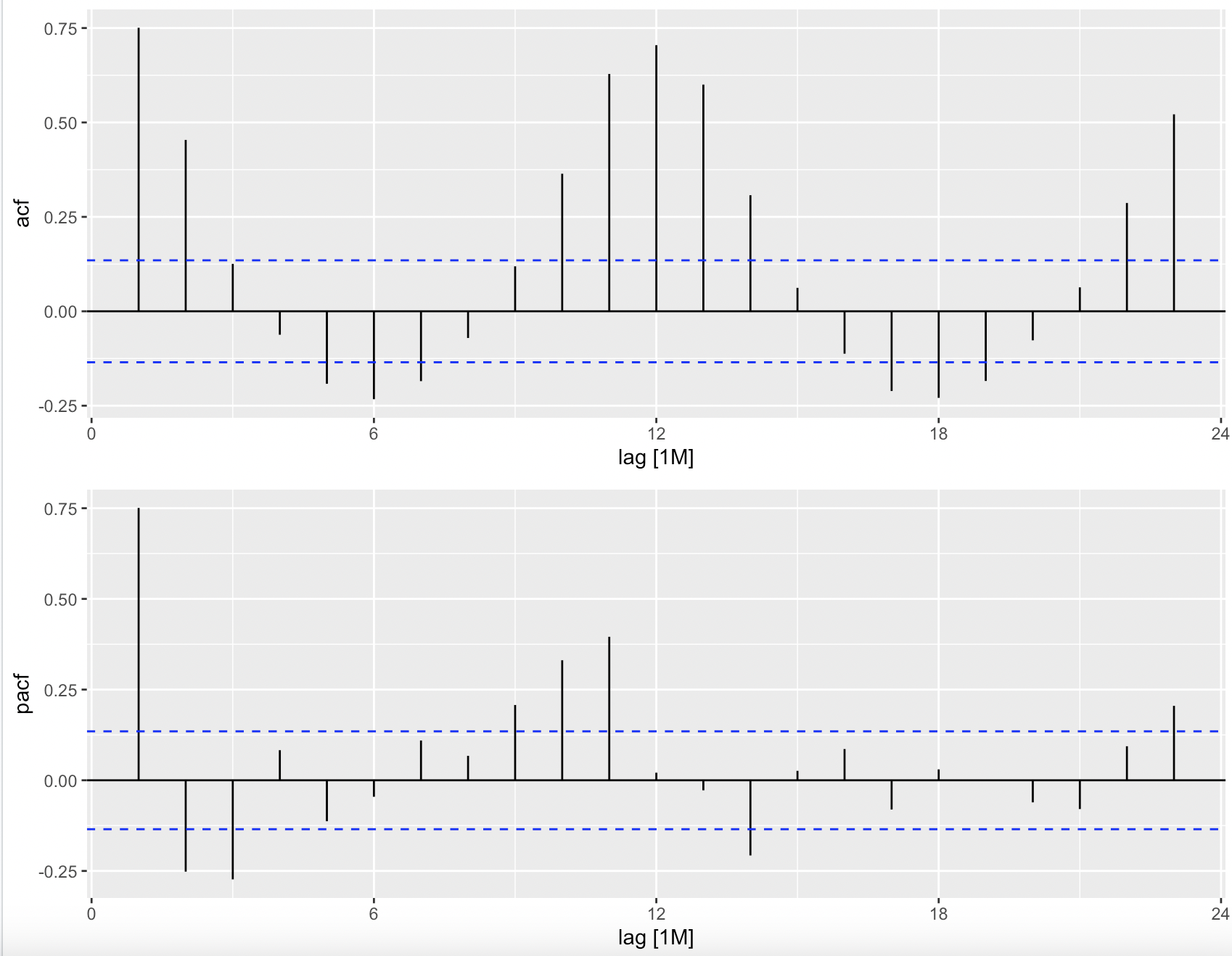
ACF 表示时间序列与其每个滞后值之间的相关系数，同时考虑到与其他滞后的关系。 PACF 虽然类似，但消除了其他每个滞后对关系的影响，因此提供了时间序列和滞后值之间更直接的相关性。
有下面两种不同的方式来查看 ACF 和 PACF 图。第一种方法使用 gridExtra 包并生成条形图，而第二种方法是使用 timetk 的散点图形式的滞后诊断图。

gridExtra::grid.arrange(
  df_ts %>% ACF(swimring) %>% autoplot(),
  df_ts %>% PACF(swimring) %>% autoplot()
)

df %>% 
  timetk::plot_acf_diagnostics(.date_var = Month,
                               .value = swimring)

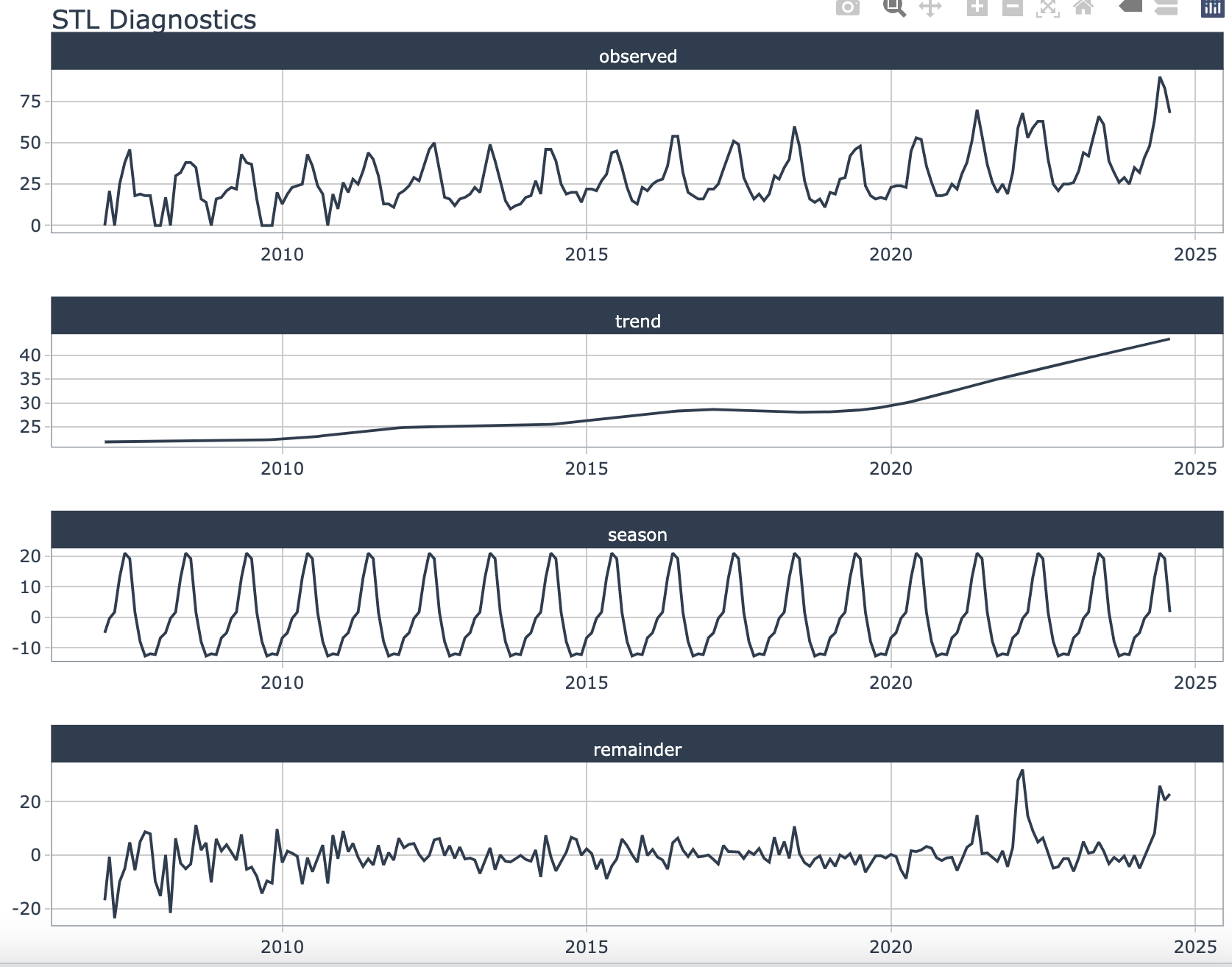
3.5 系列分解

将时序数据分解为趋势、季节性和残差三个部分。这一步可以帮助我们更好地理解数据的组成部分，并为后续的模型预测提供依据。

df %>% 
  timetk::plot_stl_diagnostics(.date_var = Month,
                               .value = swimring,
                               .facet_scales = "free",
                               .feature_set = c("observed","trend","season","remainder"))

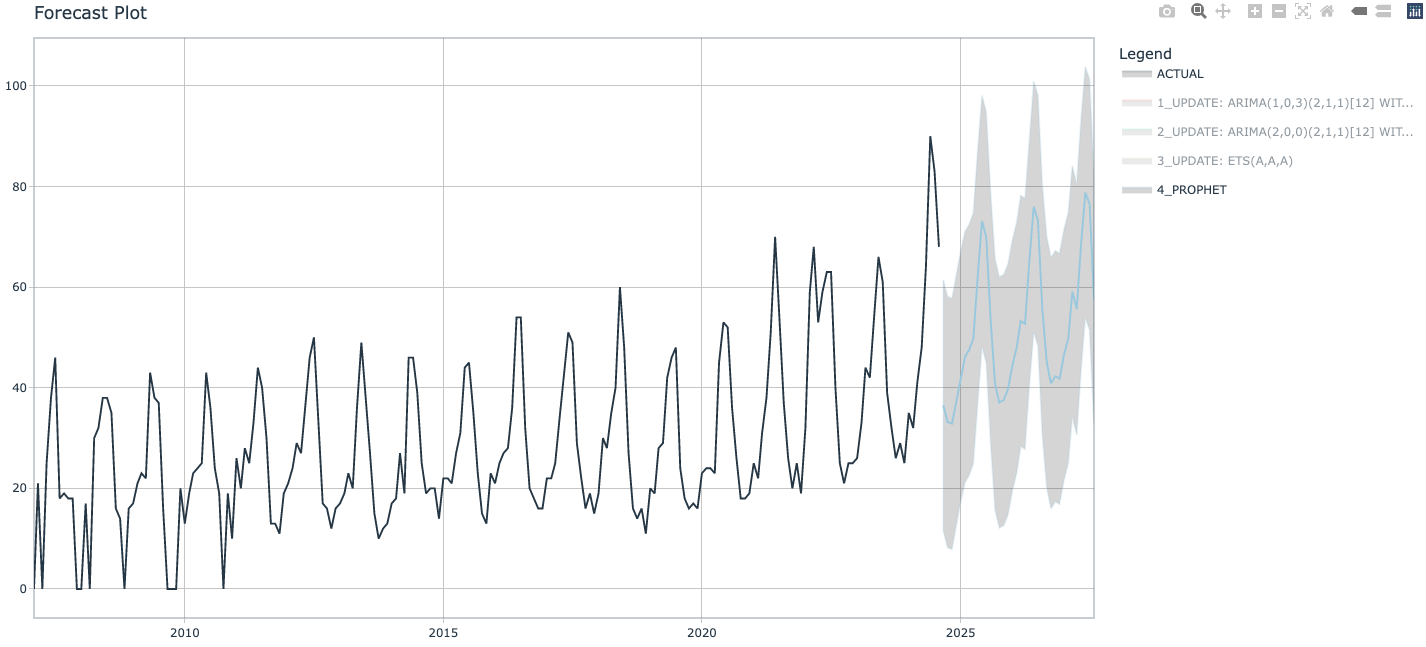
3.6 模型预测

选择合适的时序预测模型（如ARIMA、 Boosted ARIMA 、Prophet等），对游泳圈热度数据进行预测。

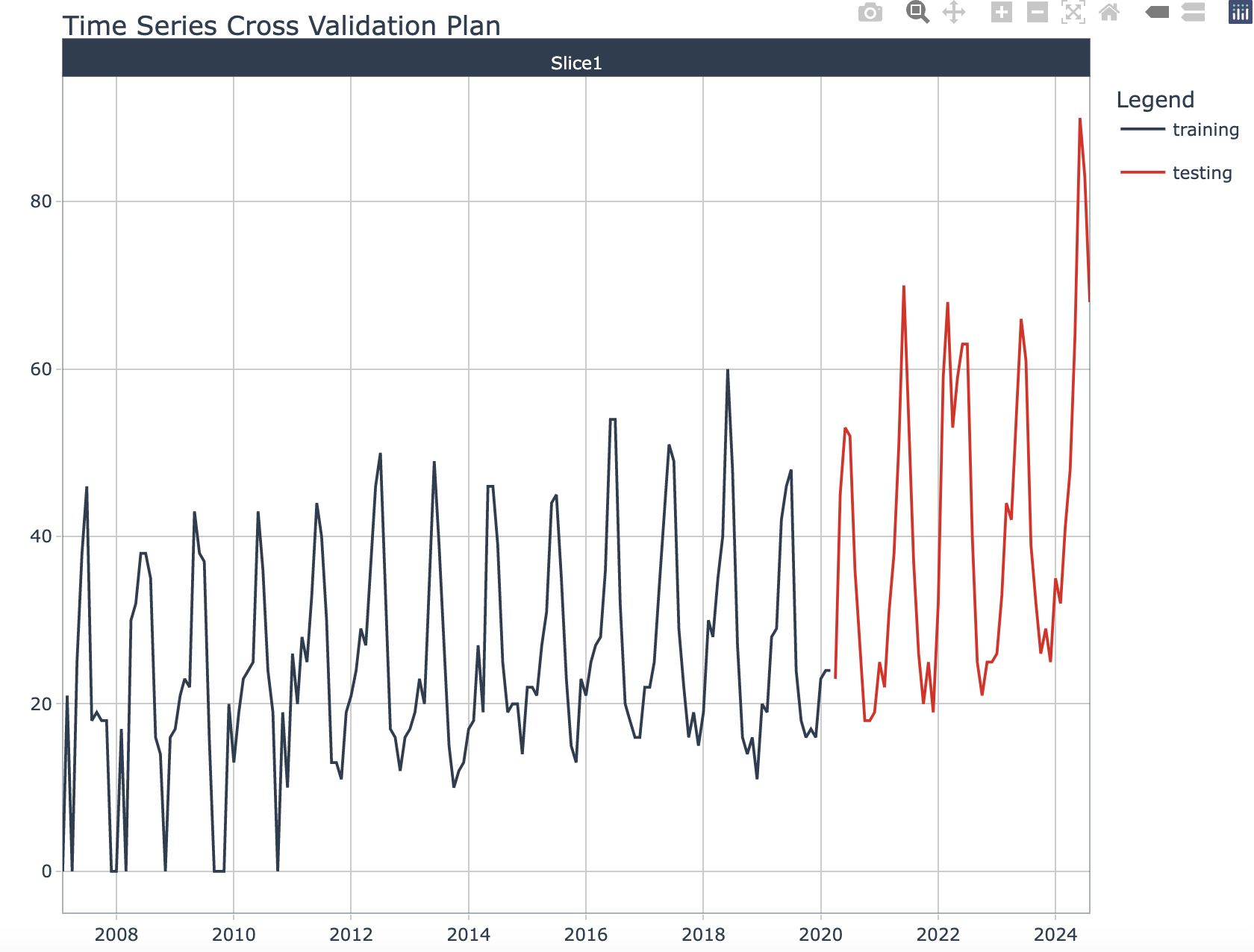
我们先来将原有的数据进行拆分，前期用作训练，后期用作预测。

splits <- initial_time_split(df)
splits %>% 
  tk_time_series_cv_plan() %>% 
  plot_time_series_cv_plan(.date_var = Month,
                           .value = swimring)

通过以下5个模型进行建模并评估结果

df_train <- training(splits)
df_test <- testing(splits)
### a. Auto ARIMA 
arima_fit <- arima_reg() %>% 
  set_engine("auto_arima") %>% 
  fit(swimring ~ Month, data = df_train)

### b. Boosted ARIMA 
arima_boost_fit <- arima_boost() %>% 
  set_engine("auto_arima_xgboost") %>% 
  fit(swimring ~ Month, data = df_train)

### c. Exponential Smoothing 
ets_fit <- exp_smoothing() %>% 
  set_engine("ets") %>% 
  fit(swimring ~ Month, data = df_train)

### d. Prophet 
prophet_fit <- prophet_reg() %>% 
  set_engine("prophet") %>% 
  fit(swimring ~ Month, data = df_train)

### e. Linear Regression
lm_fit <- linear_reg() %>% 
  set_engine("lm") %>% 
  fit(swimring ~ Month, data = df_train)

models_tbl <- modeltime_table(
  arima_fit,
  arima_boost_fit,
  ets_fit,
  lm_fit,
  prophet_fit
)

calibrate_tbl <- models_tbl %>% 
  modeltime_calibrate(new_data = df_test)

calibrate_tbl %>% 
  modeltime_forecast(
    actual_data = df,
    new_data = df_test
  ) %>% 
  plot_modeltime_forecast()

calibrate_tbl %>% 
  modeltime_accuracy()

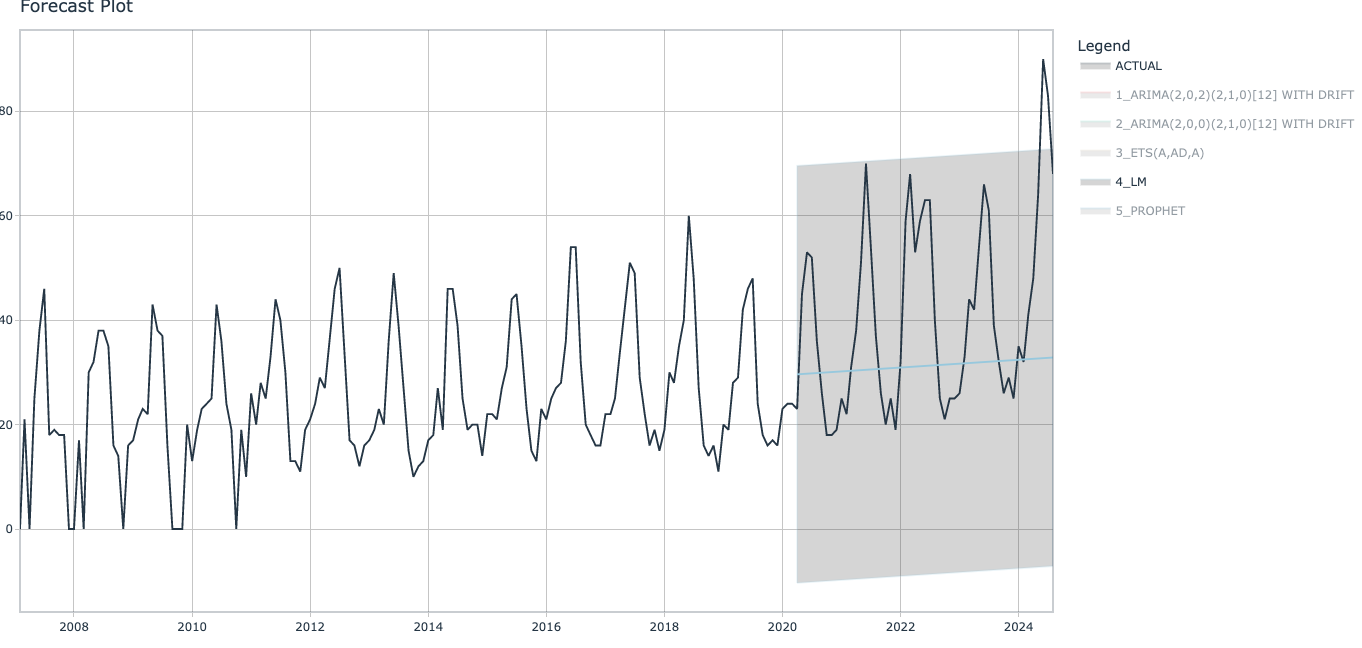
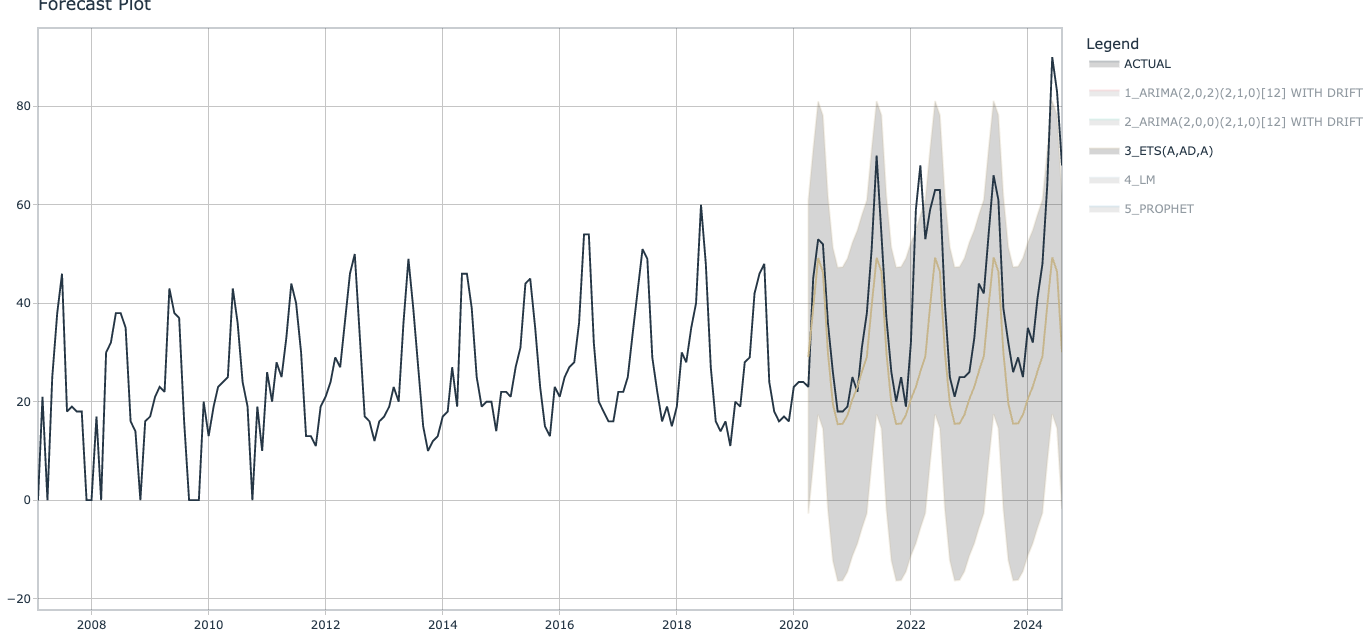
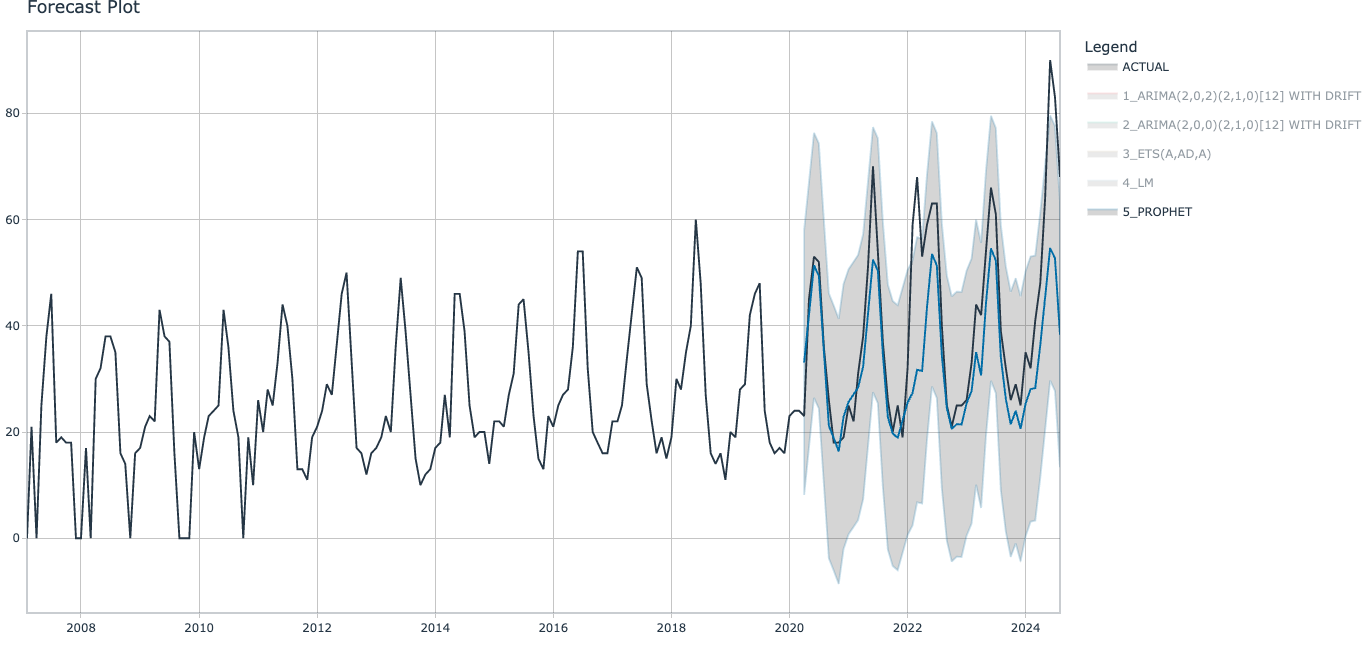
我们可以看到这些模型大部份表现都不错。 Prophet 模型具有最高的 R 平方 (0.752) 和最低的误差值 (12.7 RMSE)，但这些数字仍然不算很高。 R 平方值越接近 1，模型越好。

3.8 未来预测

利用训练好的模型对未来一段时间的游泳圈热度进行预测。通过这些预测结果，我们可以提前规划广告投入时间和资源配置。

# 去掉刚刚看到表现最差的模型
models_tbl <- modeltime_table(
  arima_fit,
  arima_boost_fit,
  ets_fit,
  prophet_fit
)

calibrate_tbl <- models_tbl %>% 
  modeltime_calibrate(new_data = df_test)

# Re-fitting
refit_tbl <- calibrate_tbl %>% 
  modeltime_refit(data = df)

# 预测后面的结果
refit_tbl %>% 
  modeltime_forecast(h = "3 years", actual_data = df) %>% 
  plot_modeltime_forecast()

根据预测结果来看，每年的3月4月游泳圈关注度急剧升高，是我们在美国市场上投流促销的好时机，6月份后关注度开始下降。

4. 总结

通过本文的时序分析与预测，我们可以更好地掌握游泳圈热度的变化规律，从而在合适的时机进行广告投入，最大化营销效果。当然可能是由于温室效应导致的气温升高促使人们越来越爱游泳了，带动了游泳圈的热度。

时序预测：利用R语言对游泳圈热度进行预测